Plantilla:Propiedades de la funcion logaritmica
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:09 8 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | + | {{Tabla75|celda1= | |
| {{Teorema_sin_demo|titulo=Propiedades de la función logarítmica|enunciado=Las funciones exponenciales de base <math>a\;</math> cumplen las siguientes propiedades: | {{Teorema_sin_demo|titulo=Propiedades de la función logarítmica|enunciado=Las funciones exponenciales de base <math>a\;</math> cumplen las siguientes propiedades: | ||
| - | *Son continuas en <math>\mathbb{R}{}_*^+</math>. | + | *Son continuas en su dominio: <math>D_f=\mathbb{R}_*^+=\mathbb{R}^+ - \{0\}</math>. |
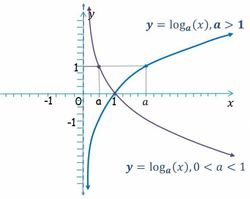
| *Pasan por <math>(1,0)\;</math> y <math>(a,1)\;</math>. | *Pasan por <math>(1,0)\;</math> y <math>(a,1)\;</math>. | ||
| - | *Si <math>a>1\;</math> son crecientes y si <math>0<a<1\;</math> son decrecientes. | + | *Crecimiento: |
| - | *Su crecimiento es menor que el de las funciones raíz de cualquier índice <math>\sqrt[n]{x}</math>. | + | :*Si <math>a>1\;</math> son crecientes. |
| + | :*Si <math>0<a<1\;</math> son decrecientes. | ||
| + | :*Su crecimiento es menor que el de las funciones raíz de cualquier índice <math>\sqrt[n]{x}</math>. | ||
| *La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta <math>y=x\;</math>. | *La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta <math>y=x\;</math>. | ||
| }} | }} | ||
| - | {{p}} | + | |celda2=[[Imagen:log_a.jpg|thumb|center|250px|Funciones logarítmicas]] |
| - | {{AI2|titulo=Actividad Interactiva: ''Propiedades de la función logar´tmica''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Comprueba las propiedades de las funciones logarítmicas en la siguiente escena. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/logaritmica_1.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/logaritmica_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | {{p}} | + | |
| - | + | ||
| - | Comprueba en la escena anterior las siguientes propiedades: | + | |
| - | + | ||
| - | * Todas pasan por los punto <math>(1,0)\;</math> y <math>(a,1)\;</math>, donde <math>a\;</math> es la base. | + | |
| - | * Si la base <math>a>1\;</math>, son crecientes y si <math>0<a<1\;</math> decrecientes. | + | |
| - | * Observa como varía la gráfica al aumentar o disminuir el valor de la base. | + | |
| - | * Las gráficas son simétricas respecto de la recta <math>y=x</math> (en rojo). | + | |
| - | + | ||
| - | Contesta: | + | |
| - | + | ||
| - | *¿Cuál es el dominio de estas funciones? o, lo que es lo mismo, ¿qué valores puede tomar la primera coordenada del punto azul? | + | |
| - | *¿Cuál es la imagen de estas funciones? o, lo que es lo mismo, ¿qué valores puede tomar la segunda coordenada del punto azul? | + | |
| - | *¿Cuál es el punto de corte de la gráfica con los ejes? | + | |
| - | }} | + | |
| }} | }} | ||
Revisión actual
Propiedades de la función logarítmica Las funciones exponenciales de base
|
 cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
 .
.
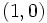 y
y 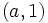 .
.
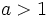 son crecientes.
son crecientes.
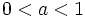 son decrecientes.
son decrecientes.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
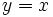 .
.