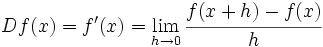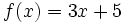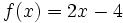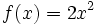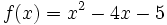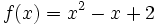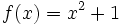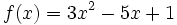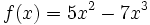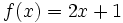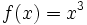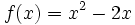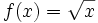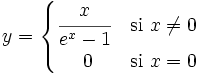Función derivada (1ºBach)
De Wikipedia
| Revisión de 23:29 27 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace2 | + | {{Menú Matemáticas 1BT |
| - | |titulo1=Función derivada primerade otra función. Reglas de derivación | + | |ir= |
| - | |duracion=9'22" | + | |ampliar= |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |repasar= |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0408.html | + | |enlaces= |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Continuidad de las funciones derivables | + | |
| - | |duracion=3'30" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0407.html | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Otra notación para la función derivada | + | |
| - | |duracion=2'56" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0410.html | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | __TOC__ | ||
| + | (Pág. 306) | ||
| + | |||
| + | {{Función derivada (1ºBach)}} | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 306)
Derivada de una función
Se llama función derivada de  , o simplemente derivada de
, o simplemente derivada de  , a una función que llamaremos
, a una función que llamaremos 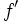 (o bien,
(o bien, 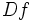 ) que asocia a cada valor
) que asocia a cada valor  , la derivada de
, la derivada de  en ese punto,
en ese punto, 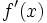 . Es decir,
. Es decir,
|
|
Notación
- Dada una función
 , la función derivada ,
, la función derivada , 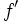 , también se llama la derivada primera de
, también se llama la derivada primera de  . También se suele representar por
. También se suele representar por 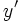 .
.
- La función derivada de
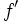 se denomina la derivada segunda de
se denomina la derivada segunda de  y se escribe
y se escribe 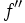 .
.
- Analogamente, tenemos la derivada tercera,
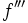 , cuarta
, cuarta 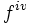 , quinta
, quinta 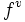 , ...
, ...
¿Qué es la derivada? Derivada de una función en un punto. Función derivada. Simulación en GeoGebra
¿Qué es la derivada? Interpretación de la derivada usando un ejemplo de Física, la velocidad puntual de un móvil.
Otra notación para la función derivada
Nota: Requiere Flash Player y ver con Firefox
Introducción al cálculo de derivadas usando la definición.
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de la siguiente función usando la definición de derivada:
Halla la derivada de las siguientes funciones usando la definición de derivada:
El universo de las derivadas
Nota: Requiere Flash Player y ver con Firefox.
Ejercicio resuelto: Función derivada
- a) Calcula la función derivada de
 . A partir de ella, calcula
. A partir de ella, calcula 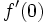 y
y 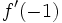 .
.
- b) Calcula la función derivada de
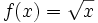 . A partir de ella, calcula
. A partir de ella, calcula 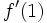 y
y 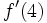 .
.
- c) Halla la ecuación de la recta tangente a la curva
 en el punto de abscisa
en el punto de abscisa 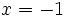 .
.
- a)
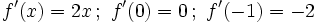
- b)
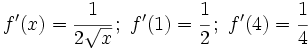
- c)
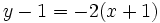
Ejercicios propuestos
|
Ejercicios propuestos: Función derivada |
Apéndice
Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda.
Nota: Requiere Flash Player y ver con Firefox