Plantilla:Función derivada (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:49 28 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:23 10 ene 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | ==Derivada de una función== | ||
| + | {{Caja_Amarilla|texto=Se llama '''función derivada de <math>f\;</math>''', o simplemente '''derivada de <math>f\;</math>''', a una función que llamaremos <math>f'\;</math> (o bien, <math>Df\;</math>) que asocia a cada valor <math>x\;</math>, la derivada de <math>f\;</math> en ese punto, <math>f'(x)\;</math>. Es decir, | ||
| + | {{p}} | ||
| + | {{Caja|contenido=<math>Df(x)=f'(x) = \lim_{h \to 0} \cfrac{f(x+h)-f(x)}{h} </math>}} | ||
| + | }} | ||
| + | {{p}} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| |titulo1=Función derivada primera de otra función. Reglas de derivación | |titulo1=Función derivada primera de otra función. Reglas de derivación | ||
Revisión de 11:23 10 ene 2017
Derivada de una función
Se llama función derivada de  , o simplemente derivada de
, o simplemente derivada de  , a una función que llamaremos
, a una función que llamaremos 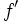 (o bien,
(o bien, 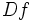 ) que asocia a cada valor
) que asocia a cada valor  , la derivada de
, la derivada de  en ese punto,
en ese punto, 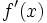 . Es decir,
. Es decir,
|
|
Definición de la función derivada de una función. Las reglas de derivación nos permiten calcular dericvadas sin calcular límites.
Función derivada de una función definida a trozos.
Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda.
Otra notación para la función derivada