Plantilla:Perpendicularidad entre rectas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:44 1 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:52 1 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio: Posición relativa de dos rectas | + | |titulo1=Ejercicio 1 |
| |duracion=3'20" | |duracion=3'20" | ||
| |sinopsis=Determina la posición relativa de las siguientes rectas: <math>L_1: 2y+12=x\;</math> y <math>L_2: -3y=6x+9\;</math> | |sinopsis=Determina la posición relativa de las siguientes rectas: <math>L_1: 2y+12=x\;</math> y <math>L_2: -3y=6x+9\;</math> | ||
| |url1=https://www.youtube.com/watch?v=61xLekGQGkk&list=PL9B9AC3136D2D4C45&index=97 | |url1=https://www.youtube.com/watch?v=61xLekGQGkk&list=PL9B9AC3136D2D4C45&index=97 | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=17' | ||
| + | |sinopsis=Determina la ecuación de las rectas que pasan por el punto P(5,7) y son paralela y perpendicular, respectivamente, a la recta determinada por los puntos C(-4,-1) y D(6,-2). | ||
| + | |url1=https://www.youtube.com/watch?v=Vqo9hm1_rjw&list=PL9B9AC3136D2D4C45&index=100 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:52 1 may 2017
Propiedad
Dos rectas, con pendientes m y m', son perpendiculares si y sólo si sus pendientes son inversas y opuestas simultaneamente:
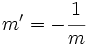
O equivalentemente, cuando el producto de ambas pendientes es igual a -1:
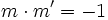
En esta escena podrás ver e interactuar con dos rectas perpendiculares y ver que las caracteriza.
Determina la posición relativa de las siguientes rectas: 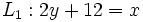 y
y 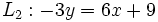
Determina la ecuación de las rectas que pasan por el punto P(5,7) y son paralela y perpendicular, respectivamente, a la recta determinada por los puntos C(-4,-1) y D(6,-2).
En esta escena podrás practicar como se halla la ecuación de la recta que pasa por un punto dado y es paralela o perpendiclar a otra recta de ecuación dada.

