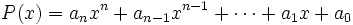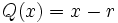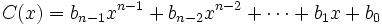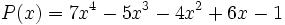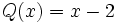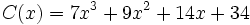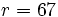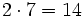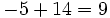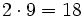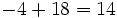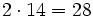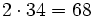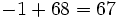Plantilla:Regla de Ruffini
De Wikipedia
| Revisión de 09:56 20 abr 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:42 2 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 95: | Línea 95: | ||
| Los valores <math>b_i\;</math> son los coeficientes del polinomio cociente <math>C(x)\;</math>, cuyo grado será un grado menor que el del dividendo <math>P(x)\;</math>. El resto será <math>s\;</math>. | Los valores <math>b_i\;</math> son los coeficientes del polinomio cociente <math>C(x)\;</math>, cuyo grado será un grado menor que el del dividendo <math>P(x)\;</math>. El resto será <math>s\;</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Regla de Ruffini | ||
| + | |duracion=10´ | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/05-regla-de-ruffini#.VCMAcxZ8HA8 | ||
| + | |sinopsis=La regla de Ruffini nos permite determinar supersónicamente el cociente y el resto de la división entre un polinomio P(x) y el polinomio Q(x) = x - a. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 142: | Línea 149: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=División de polinomios por Ruffini | + | |titulo1=Ejemplo 1: ''División de polinomios por Ruffini'' |
| |duracion=5'14" | |duracion=5'14" | ||
| |sinopsis=Ejemplo de división de polinomios usando la regla de Ruffini. | |sinopsis=Ejemplo de división de polinomios usando la regla de Ruffini. | ||
| Línea 149: | Línea 156: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Regla de Ruffini | + | |titulo1=Ejemplos 2: ''División de polinomios por Ruffini'' |
| - | |duracion=10´ | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/05-regla-de-ruffini#.VCMAcxZ8HA8 | + | |
| - | |sinopsis=La regla de Ruffini nos permite determinar supersónicamente el cociente y el resto de la división entre un polinomio P(x) y el polinomio Q(x) = x - a. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace | + | |
| - | |titulo1=2 ejemplos de división mediante la regla de Ruffini | + | |
| |duracion=7´ | |duracion=7´ | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/0501-dos-ejercicios-2#.VCMBFBZ8HA8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/0501-dos-ejercicios-2#.VCMBFBZ8HA8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=2 ejemplos de división mediante la regla de Ruffini |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Otros 2 ejemplos de aplicación de la regla de Ruffini | + | |titulo1=Ejemplos 3: ''División de polinomios por Ruffini'' |
| |duracion=7´ | |duracion=7´ | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/0502-dos-ejercicios-5#.VCMBoRZ8HA8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/0502-dos-ejercicios-5#.VCMBoRZ8HA8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Otros 2 ejemplos de aplicación de la regla de Ruffini |
| }} | }} | ||
| + | {{Video_enlace_juliopofe | ||
| + | |titulo1=Problema | ||
| + | |duracion=8'59" | ||
| + | |sinopsis=Hallar el punto de intersección de dos funciones polinómicas | ||
| + | |url1=https://www.youtube.com/watch?v=2CY0oR_UqfA | ||
| + | }} | ||
| + | {{p}} | ||
Revisión de 12:42 2 may 2017
Regla de Ruffini
La Regla de Ruffini es un procedimiento que nos permite dividir un polinomio entre un binomio de la forma 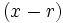 , siendo
, siendo  un número entero.
un número entero.
Debemos esta regla al matemático italiano Paolo Ruffini,
Nota: Lo que sigue no es una demostración, sino el proceso que hay que seguir para aplicar la regla.
Vamos a dividir el polinomio
entre el binomio
para obtener el cociente
y el resto 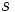 .
.
1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de  y los escribimos ordenados. Entonces escribimos
y los escribimos ordenados. Entonces escribimos  en la parte inferior izquierda del eje, encima de la línea:
en la parte inferior izquierda del eje, encima de la línea:
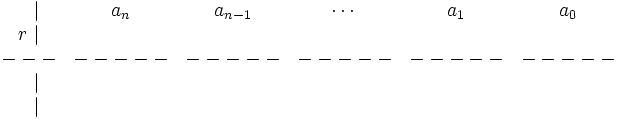
2. Pasamos el coeficiente más pegado a la izquierda,  , justo debajo de la línea, para obtener el primero de los coeficientes
, justo debajo de la línea, para obtener el primero de los coeficientes 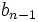 :
:
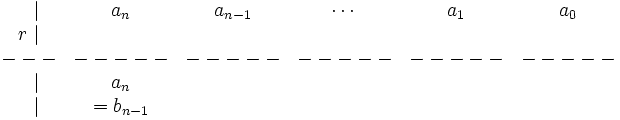
3. Multiplicamos el número más pegado a la derecha debajo de la línea por  y lo escribimos sobre la línea en la primera posición de la derecha:
y lo escribimos sobre la línea en la primera posición de la derecha:
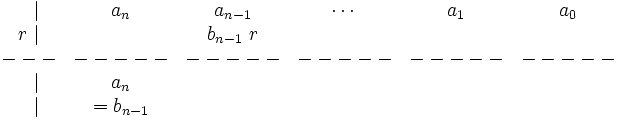
4. Añadimos los dos valores que hemos puesto en la misma columna:
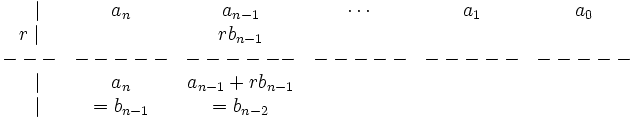
5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:
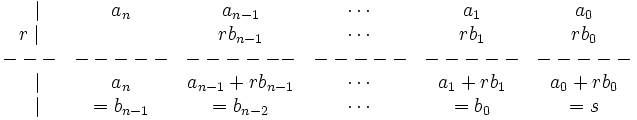
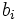 son los coeficientes del polinomio cociente
son los coeficientes del polinomio cociente 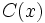 , cuyo grado será un grado menor que el del dividendo
, cuyo grado será un grado menor que el del dividendo  . El resto será
. El resto será 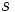 .
.La regla de Ruffini nos permite determinar supersónicamente el cociente y el resto de la división entre un polinomio P(x) y el polinomio Q(x) = x - a.
Ejemplo: Regla de Ruffini
Divide los polinomios usando la regla de Ruffini:
| 7 -5 -4 6 -1
|
2| 14 18 28 68
--|-------------------
| 7 9 14 34 |67
|____
El resultado significa que:
|
|
Ejemplo de división de polinomios usando la regla de Ruffini.
2 ejemplos de división mediante la regla de Ruffini
Otros 2 ejemplos de aplicación de la regla de Ruffini