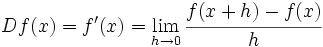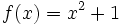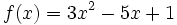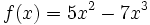Plantilla:Función derivada (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:54 2 may 2017 Coordinador (Discusión | contribuciones) (→Derivada de una función) ← Ir a diferencia anterior |
Revisión de 17:54 2 may 2017 Coordinador (Discusión | contribuciones) (→Derivada de una función) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Función derivada''|enunciado= | + | {{Ejemplo|titulo=Ejercicio resuelto: ''Función derivada''|enunciado= |
| :a) Calcula la función derivada de <math>f(x)=x^2\;</math>. A partir de ella, calcula <math>f'(0)\;</math> y <math>f'(-1)\;</math>. | :a) Calcula la función derivada de <math>f(x)=x^2\;</math>. A partir de ella, calcula <math>f'(0)\;</math> y <math>f'(-1)\;</math>. | ||
Revisión de 17:54 2 may 2017
Derivada de una función
Se llama función derivada de 
, o simplemente derivada de , a una función que llamaremos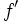 
(o bien, 
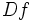) que asocia a cada valor 
, la derivada de en ese punto,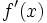 
. Es decir,
|
|
Notación:
- Dada una función y=f(x), la función derivada , 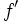también se llama la derivada primera de . También se suele representar por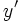
.
- La función derivada de 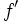se denomina la derivada segunda de y se escribe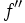
.
- Analogamente, tenemos la derivada tercera,
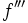, cuarta 
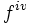, quinta 
, ...
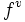Otra notación para la función derivada (2'56") Sinopsis: Otra notación para la función derivada
Ejemplo 1 (9'24") Sinopsis: Halla la derivada de la siguiente función usando la definición de derivada:
Ejemplo 2 (6'44") Sinopsis: Halla la derivada de la siguiente función usando la definición de derivada:
Ejemplo 3 (13'20") Sinopsis: Halla la derivada de la siguiente función usando la definición de derivada:
Ejercicio resuelto: Función derivada
- a) Calcula la función derivada de
. A partir de ella, calcula 
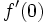y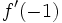 
.
- b) Calcula la función derivada de
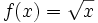. A partir de ella, calcula 
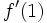y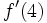 
.
- c) Halla la ecuación de la recta tangente a la curva en el punto de abscisa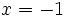
.
Solución:
- a)
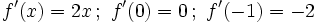
- b)
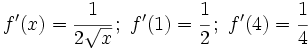
- c)
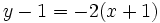
Ejercicios propuestos
 Ejercicios propuestos: Función derivada (pág. 306-307)
|
Para ampliar
Derivada de una función definida a trozos (10'49") Sinopsis: Función derivada de una función definida a trozos.
Continuidad de las funciones derivables (3'30") Sinopsis: Teorema que relaciona la existencia de derivadas laterales y la continuidad de una función por la derecha y por la izquierda.
