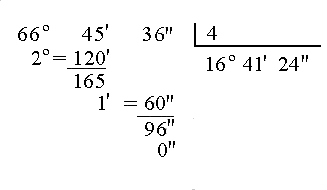Plantilla:Operaciones con ángulos
De Wikipedia
| Revisión de 20:09 6 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:13 6 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | |||
| - | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás ver como se opera con ángulos gráficamente y algebraicamente. | ||
| - | |enlace=[https://ggbm.at/KvpBsX52 Operaciones con ángulos] | ||
| - | }} | ||
| - | {{p}} | ||
| ===Suma=== | ===Suma=== | ||
| La medida del tiempo, igual que los ángulos, se realiza en el sistema sexagesimal. Analicemos el siguiente ejemplo: | La medida del tiempo, igual que los ángulos, se realiza en el sistema sexagesimal. Analicemos el siguiente ejemplo: | ||
| Línea 143: | Línea 137: | ||
| :c) 125º 15' 30" : 3 | :c) 125º 15' 30" : 3 | ||
| |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo8.htm | |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo8.htm | ||
| + | }} | ||
| + | ===Actividades=== | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver como se opera con ángulos gráficamente y algebraicamente. | ||
| + | |enlace=[https://ggbm.at/KvpBsX52 Operaciones con ángulos] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_enlace|titulo1=Actividad Interactiva: ''Ángulos complementarios y suplementarios'' | ||
| + | |descripcion=Calcula los ángulos complementario y suplementario de los siguientes: | ||
| + | |||
| + | :a) 56º 20' 40" | ||
| + | |||
| + | :b) 37º 42' 15" | ||
| + | |||
| + | :c) 125º 15' 30" | ||
| + | |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo9.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 1 | ||
| + | |duracion=3'45" | ||
| + | |sinopsis=¿Cuál es el complementario de 53º41'28" | ||
| + | |url1=https://www.youtube.com/watch?v=zIUtvfczPa8 | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 2 | ||
| + | |duracion=3'43" | ||
| + | |sinopsis=¿Cuál es el suplementario de 75º16'49" | ||
| + | |url1=https://www.youtube.com/watch?v=UVxyZ0-8MDY | ||
| }} | }} | ||
Revisión de 20:13 6 may 2017
Tabla de contenidos |
Suma
La medida del tiempo, igual que los ángulos, se realiza en el sistema sexagesimal. Analicemos el siguiente ejemplo:
Ejemplo: Suma en el sistema sexagesimal
- Luis es un corredor de maratón que para entrenarse corrió dos días seguidos una maratón. Obtuvo los siguientes registros: el primer día corrió la maratón en 2 h 48 min 35 s; el segundo día, en 2 h 45 min 30 s. ¿Cuánto tiempo corrió Luis en ambos días?
Si sumamos por separado las horas, los minutos y los segundos, resulta:
2 h 48 min 35 s + 2 h 45 min 30 s ___________________ 4 h 93 min 65 s
Pero 65 segundos equivalen a 1 minuto (60 segundos) y 5 segundos, luego la suma se puede escribir así:
4 h 94 min 5 s
De la misma forma, 94 min equivalen a 1 hora y 34 minutos. Luego la suma es:
5 h 34 min 5 s
Los mismos procedimientos hay que realizar para sumar ángulos.
Actividad Interactiva: Suma de ángulos Descripción: Realiza en tu cuaderno las siguientes sumas de ángulos:
- a) 56º 20' 40" + 37º 42' 15"
- b) 125º 15' 30" + 24º 50' 40"
- c) 33º 33' 33" + 17º 43' 34"
Resta
Para restar tendremos en cuenta las mismas consideraciones que para sumar. Analicemos el siguiente ejemplo:
Ejemplo: Resta en el sistema sexagesimal
- En la primera carrera, Luis había tardado 2 h 48 min 35 s y su compañero corrió la maratón en 3 horas exactamente. ¿Cuál es la diferencia de tiempo entre ambos?
Debemos hacer la siguiente operación:
3 h 0 min 0 s − 2 h 48 min 35 s ___________________
Igual que en la suma, deberíamos restar por separado las horas los minutos y los segundos, pero no podemos hacer las restas 0-35 (segundos) ni 0-48 (minutos). Para conseguirlo transformamos una hora en 60 minutos y un minuto en 60 segundos. Es decir, las 3 horas se convierten en 2h 59' 60".
2 h 60 min 60 s − 2 h 48 min 35 s ___________________ 0 h 11 min 25 s
Actividad Interactiva: Resta de ángulos Descripción: Realiza en tu cuaderno las siguientes restas de ángulos:
- a) 56º 20' 40" - 37º 42' 15"
- b) 125º 15' 30" - 24º 50' 40"
- c) 33º 33' 33" - 17º 43' 34"
Multiplicación por un número natural
Para multiplicar un ángulo por un número natural debemos multiplicar por ese número cada una de las unidades del ángulo (grados, minutos y segundos). Si alguno de los productos de los segundos o minutos es superior a 60, lo transformamos en una unidad de orden inmediatamente superior.
Analicemos el siguiente ejemplo:
Ejemplo: Producto por un número en el sistema sexagesimal
- Multiplica 18º 26' 35" por 3.
18º 26' 35" x 3 _______________ 54º 78' 105"
Pero 105" = 1' 45", luego
54º 79' 45"
Pero 79' = 1º 19', luego
55º 19' 45"
Realiza en tu cuaderno las siguientes multiplicaciones de ángulos:
- a) 56º 20' 40" x 2
- b) 37º 42' 15" x 4
- c) 125º 15' 30" x 3
División por un número natural
Para dividir un ángulo por un número natural dividimos los grados entre ese número. Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos. Dividimos los minutos. Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. Dividimos los segundos.
Analicemos el siguiente ejemplo:
Ejemplo: División por un número en el sistema sexagesimal
- Divide 66º 45' 36" entre 4.
Realiza en tu cuaderno las siguientes divisiones de ángulos:
- a) 56º 20' 40" : 5
- b) 37º 42' 15" : 4
- c) 125º 15' 30" : 3
Actividades
Operaciones con ángulos Descripción: En esta escena podrás ver como se opera con ángulos gráficamente y algebraicamente.
Calcula los ángulos complementario y suplementario de los siguientes:
- a) 56º 20' 40"
- b) 37º 42' 15"
- c) 125º 15' 30"
Ejemplo 1 (3'45") Sinopsis: ¿Cuál es el complementario de 53º41'28"
Ejemplo 2 (3'43") Sinopsis: ¿Cuál es el suplementario de 75º16'49"
