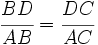Plantilla:Aplicaciones de los criterios de semejanza
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:14 7 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:20 7 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 17: | Línea 17: | ||
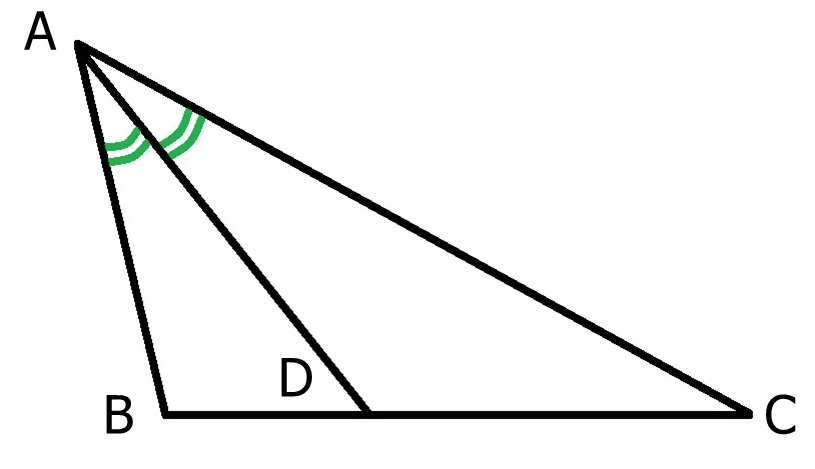
| |sinopsis=El teorema de la bisectriz dice: | |sinopsis=El teorema de la bisectriz dice: | ||
| :"La bisectriz de un ángulo de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo" | :"La bisectriz de un ángulo de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo" | ||
| + | :<math>\cfrac{BD}{AB}=\cfrac{DC}{AC}</math>[[Imagen:teobisectriz.jpg]] | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
Revisión de 10:20 7 may 2017
Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas.
Medición de alturas con espejos Descripción: En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica.
Medición de alturas con sombras Descripción: Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura..
Teorema de la bisectriz (8´43") Sinopsis: El teorema de la bisectriz dice:
- "La bisectriz de un ángulo de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo"
Problema (Teorema de la bisectriz) (5´46") Sinopsis: Aplicación del teorema de la bisectriz.
