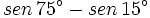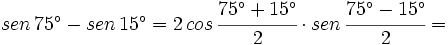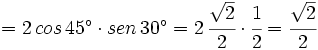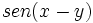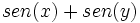Fórmulas trigonométricas (1ºBach)
De Wikipedia
| Revisión de 16:39 7 may 2017 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de la suma de dos ángulos) ← Ir a diferencia anterior |
Revisión de 16:52 7 may 2017 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) Ir a siguiente diferencia → |
||
| Línea 327: | Línea 327: | ||
| }} | }} | ||
| - | ==Ejercicios propuestos== | + | ==Ejercicios== |
| + | |||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Identidades trigonométricas|enunciado= | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=2´48" | ||
| + | |url1=https://www.youtube.com/watch?v=8ESRmd-i_qs | ||
| + | |sinopsis=Comprueba la siguiente identidad trigonométrica: | ||
| + | |||
| + | <math>4 \,sen^2 \alpha \cdot cos^2 \alpha = 1 - cos^2 (2\alpha)\;</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Fórmulas trigonométricas'' | |titulo=Ejercicios propuestos: ''Fórmulas trigonométricas'' | ||
Revisión de 16:52 7 may 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
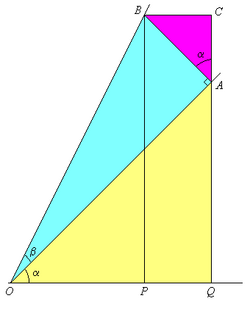
Razones trigonométricas de la suma de dos ángulos
Razones trigonométricas de la suma de dos ángulos
I.1: 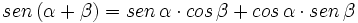
I.2: 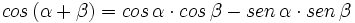
I.3: 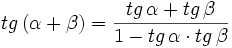
Fórmulas trigonométricas de la suma de dos ángulos con demostración.
Ejemplo: Razones trigonométricas de la suma de dos ángulos
Calcula el valor exacto de 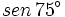 (sin calculadora)
(sin calculadora)
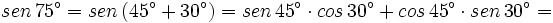
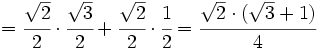
Halla el valor exacto de 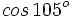 .
.
Halla el valor exacto de 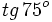 .
.
Hallar las razones trigonométricas de θ + μ sabiendo que θ y μ son del segundo cuadrante y que senθ = 1 / 2 y que cosμ = − 2 / 3.
Demostrar que si A+B+C=180º, entonces tg A + tg B + tg C = tg A · tg B · tg C.
Seno, coseno y tangente de la suma de tres ángulos.
Razones trigonométricas de la diferencia de dos ángulos
Razones trigonométricas de la diferencia de dos ángulos
II.1: 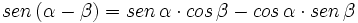
II.2: 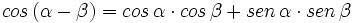
II.3: 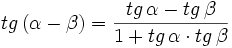
Para las demostraciones basta sustituir 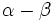 por
por 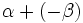 y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:
y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:
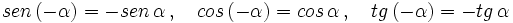
Fórmulas trigonométricas de la diferencia de dos ángulos con demostración.
Ejemplo: Razones trigonométricas de la diferencia de dos ángulos
Calcula el valor exacto de 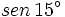 (sin calculadora)
(sin calculadora)
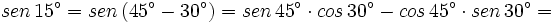
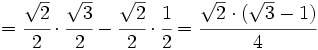
Obtención del valor exacto de sen 15º a partir de la fórmula del seno del ángulo diferencia.
Obtención del valor exacto de 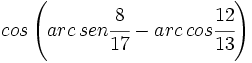 .
.
Razones trigonométricas del ángulo doble
Razones trigonométricas del ángulo doble
III.1: 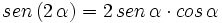
III.2: 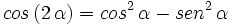
III.3: 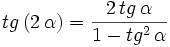
Basta utilizar las fórmulas de la suma (I.1, I.2 y I.3) y hacer
 .
.Ejemplo: Razones trigonométricas del ángulo doble
Calcula el valor de 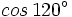 a partir de las razones trigonométricas de 60º.
a partir de las razones trigonométricas de 60º.
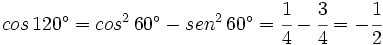
Si 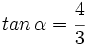 y
y 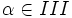 , halla el valor exacto de
, halla el valor exacto de 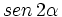 .
.
Razones trigonométricas del ángulo mitad
Razones trigonométricas del ángulo mitad
IV.1: 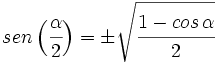
IV.2: 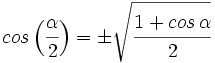
IV.3: 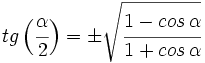
Teniendo en cuenta que 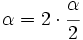 y utilizando la fórmula III.2 del coseno del ángulo doble, tenemos:
y utilizando la fórmula III.2 del coseno del ángulo doble, tenemos:
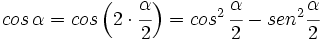
que combinado con la fórmula fundamental, nos da el siguiente sistema:
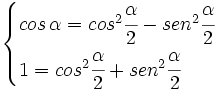
Sumando y restando ambas ecuaciones, tenemos las siguientes expresiones:
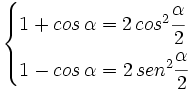
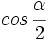 y
y 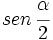 , y a partir de ellos, se obtiene el valor de
, y a partir de ellos, se obtiene el valor de 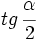 .
.Fórmulas trigonométricas del ángulo doble y del ángulo mitad con demostración.
Ejemplo: Razones trigonométricas del ángulo mitad
Calcula el valor exacto de 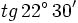 (sin calculadora).
(sin calculadora).
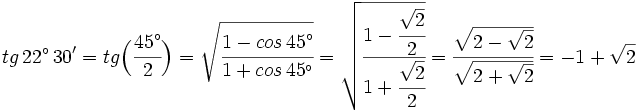
- Determinar el sen3θ en función del senθ.
- Determinar el cos3θ en función del cosθ.
Si μ es un ángulo del tercer cuadrante, y tgμ = 3, determinar las razones trigonométricas de μ / 2.
Transformaciones de sumas y diferencias de senos y cosenos en productos
Transformaciones de sumas en productos
V.1: 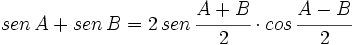
V.2: 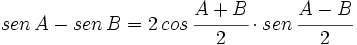
V.3: 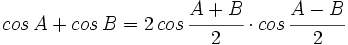
V.4: 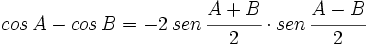
V.1 y V.2:
Partiendo de las expresiones del I.1 y II.1 del seno de una suma y de una diferencia:
- I.1:
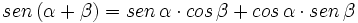
- II.1:
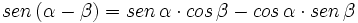
Sumando y restando ambas expresiones, obtenemos:
- Sumando:
 [1]
[1]
- Restando:
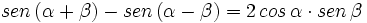 [2]
[2]
Hacemos los siguientes cambios de variable:

Resolviendo este sistema:
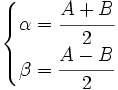
Fórmulas trigonométricas de la transformación de la suma o diferencia en producto con demostración.
Ejercicios
Comprueba la siguiente identidad trigonométrica:
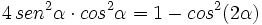
Ejercicios propuestos
|
Ejercicios propuestos: Fórmulas trigonométricas |
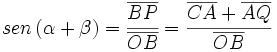
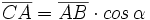
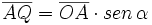
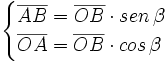
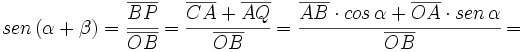
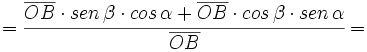
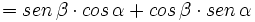
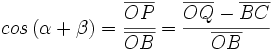
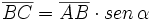
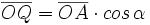
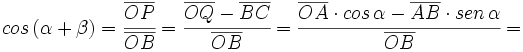
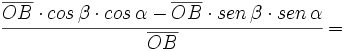
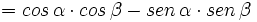
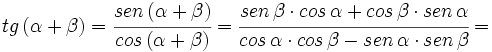
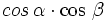 )
)