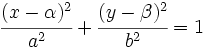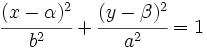La elipse (1ºBach)
De Wikipedia
| Revisión de 18:00 31 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ecuación de la elipse con el centro desplazado del origen de coordenadas) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==La elipse== | ||
| + | {{Caja_Amarilla|texto=Dados dos puntos <math>F\,</math> y <math>F'\,</math> llamados '''focos''', y una distancia <math>k\,</math>, llamada '''constante de la elipse''' (<math>k > d(F,F')\,</math>), se llama '''elipse''' al lugar geométrico de los puntos <math>P\,</math> del plano cuya suma de distancias a los focos es igual a <math>k\,</math>: | ||
| + | |||
| + | {{Caja|contenido=<math>\big \{P(x,y) \, / \; d(P,F)+d(P,F')=k \big \}</math>}} | ||
| + | |||
| + | }} | ||
| + | |||
| ==Elementos de la elipse== | ==Elementos de la elipse== | ||
| {{Tabla75|celda2=[[Imagen:Elipse.png]] | {{Tabla75|celda2=[[Imagen:Elipse.png]] | ||
| |celda1= | |celda1= | ||
| - | {{Caja Amarilla|texto=Una una elipse de '''focos''' <math>F\,</math> y <math>F'\,</math>, con '''ejes''' de simetría <math>AA'\,</math> y <math>BB'\,</math>, que se cortan en el '''centro''' <math>O\,</math> de la elipse, determina los siguientes segmentos: | + | {{Caja Amarilla|texto=Una elipse de '''focos''' <math>F\,</math> y <math>F'\,</math>, con '''ejes''' de simetría <math>AA'\,</math> y <math>BB'\,</math>, que se cortan en el '''centro''' <math>O\,</math> de la elipse, determina los siguientes segmentos: |
| {{p}} | {{p}} | ||
| - | *{{Sube|porcentaje=+20%|contenido=<math>a=\overline{OA}=\overline{OA'}</math>}} '''(semieje mayor)'''. | + | *'''Semieje mayor:''' {{Sube|porcentaje=+20%|contenido=<math>a=\overline{OA}=\overline{OA'}</math>}}. |
| - | *{{Sube|porcentaje=+20%|contenido=<math>b=\overline{OB}=\overline{OB'}</math>}} '''(semieje menor)'''. | + | *'''Semieje menor:''' {{Sube|porcentaje=+20%|contenido=<math>b=\overline{OB}=\overline{OB'}</math>}}. |
| - | *{{Sube|porcentaje=+20%|contenido=<math>c=\overline{OF}=\overline{OF'}</math>}} '''(semidistancia focal)'''. | + | *'''Semidistancia focal:''' {{Sube|porcentaje=+20%|contenido=<math>c=\overline{OF}=\overline{OF'}</math>}}. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 41: | Línea 48: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Propiedad de la elipse''|cuerpo= | + | {{Video_enlace_julioprofe |
| - | {{ai_cuerpo | + | |titulo1=Trazado de una elipse y elementos principales |
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco. | + | |duracion=5'20" |
| - | + | |sinopsis=Trazado de una elipse y elementos principales. | |
| - | |actividad= | + | |url1=https://www.youtube.com/watch?v=81NbgFpAfOU |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_5.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_5.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicios:''' | + | |
| - | *Desliza el punto verde hacia arriba. | + | |
| - | **Describe lo que ves. | + | |
| - | *Utiliza el segundo deslizador para cambiar la dirección del "rayo" y repite la animación. Prueba a modificar también la forma de la elipse (arrastrando sus vértices). | + | |
| - | **¿Qué se puede decir de los rayos que salen de un foco de cualquier elipse y se reflejan en ella? | + | |
| - | *Arrastra el vértice derecho de la elipse hasta conseguir una circunferencia (elipse de excentricidad 0) y observa: | + | |
| - | ** ¿Qué ocurre con un rayo emitido desde el radio de una circunferencia reflejado en ella misma? | + | |
| - | ** ¿Qué ángulo forman el radio de una circunferencia y la tangente a la misma en el punto correspondiente? | + | |
| }} | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco. | ||
| + | |enlace=[https://ggbm.at/n4uwXebx Propiedad de la elipse] | ||
| }} | }} | ||
| + | {{p}} | ||
| ==Excentricidad de la elipse== | ==Excentricidad de la elipse== | ||
| - | {{Caja Amarilla|texto=La '''escentricidad''' es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. | + | {{Caja Amarilla|texto=La excentricidad de la elipse es el cociente entre la distancia focal y el eje mayor: |
| - | + | ||
| - | La excentricidad de la elipse es el cociente entre la distancia focal y el eje mayor: | + | |
| <center><math>e=\cfrac{c}{a}</math></center> | <center><math>e=\cfrac{c}{a}</math></center> | ||
| Línea 75: | Línea 69: | ||
| {{p}} | {{p}} | ||
| {{Teorema|titulo=Propiedades|enunciado= | {{Teorema|titulo=Propiedades|enunciado= | ||
| - | *<math>0<e<1\,</math>. | + | *En una elipse <math>0<e<1\,</math>. |
| *Una elipse más se parece a a una circunferencia, cuanto más se aproxime a 0 su excentricidad. | *Una elipse más se parece a a una circunferencia, cuanto más se aproxime a 0 su excentricidad. | ||
| |demo= | |demo= | ||
| Línea 85: | Línea 79: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Excentricidad de la elipse''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=En la siguiente escena vamos a ver como se ve afectada la elipse si modificamos su excentricidad. |
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver como se ve afectada la elipse si modificamos su excentricidad. | + | |enlace=[https://ggbm.at/bgszwjdz Excentricidad de la elipse] |
| - | + | ||
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_4.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_4.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicios:''' | + | |
| - | #¿A qué se le llama excentricidad de una elipse? ¿Es correcto el valor de la excentricidad de la elipse de la figura? | + | |
| - | #Modifica el valor de e (deslizando el punto verde) y observa los cambios. | + | |
| - | ##¿Entre qué valores puede variar la excentricidad de una elipse? | + | |
| - | ##¿Cómo son las elipses de excentricidad grande (próxima a 1)? ¿Y la elipse de excentricidad 0? | + | |
| - | ##¿Sabías que la Tierra da vueltas alrededor del Sol describiendo una órbita elíptica de excentricidad 0.016751? Aproxima a ese valor el de la excentricidad de la elipse de la figura. ¿Describe la figura resultante. ¿Dónde crees que se sitúa el Sol? | + | |
| - | ##Los planetas de nuestro Sistema Solar cuya órbita tiene mayor excentricidad son Marte (e=0.09) y Plutón (e=0.25). Comprueba qué aspecto tiene dichas órbitas. | + | |
| - | #Pulsa el botón Actualizar para recuperar la imagen inicial. Modifica el valor de a y observa los cambios. | + | |
| - | ##¿Qué tienen en común todas las elipses con la misma excentricidad? | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 117: | Línea 91: | ||
| {{Caja|contenido=<math>\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1</math>}} | {{Caja|contenido=<math>\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1</math>}} | ||
| - | |demo=Sean <math>F(-c,0)\,</math> y <math>F'(c,0)\,</math> los focos de la elipse. Cualquier punto P(x,y) de la misma cumple: | + | |demo=Sean <math>F(c,0)\,</math> y <math>F'(-c,0)\,</math> los focos de la elipse. Cualquier punto P(x,y) de la misma cumple: |
| {{p}} | {{p}} | ||
| <center><math>d(P,F)+d(P,F')=2a\,</math></center> | <center><math>d(P,F)+d(P,F')=2a\,</math></center> | ||
| Línea 155: | Línea 129: | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Ecuación reducida de la elipse''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9. | ||
| - | |actividad=La ecuación reducida viene dada por la fórmula: | ||
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1</math></center> | + | {{Video_enlace_unicoos |
| + | |titulo1=Ejemplo | ||
| + | |duracion=7'36" | ||
| + | |sinopsis=Ecuación reducida de la elipse de eje mayor 40 y distancia focal 24 | ||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/conicas/elipse/elipse-01 | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | Sustituyendo a=5 y b=3, tenemos: | + | {{Geogebra_enlace |
| - | {{p}} | + | |descripcion=En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9. |
| - | <center><math>\cfrac{x^2}{25}+\cfrac{y^2}{9}=1</math></center> | + | |enlace=[https://ggbm.at/KX5YZAqA Ecuación reducida de la elipse] |
| - | {{p}} | + | |
| - | Puedes ver su gráfica en la siguente escena: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_2.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicio:''' | + | |
| - | #Halla la ecuación reducida de la elipse cuyos ejes miden 16 y 10. Comprueba los resulatados en la escena | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| ===Ecuación de la elipse con los focos en el eje Y=== | ===Ecuación de la elipse con los focos en el eje Y=== | ||
| - | {{Teorema_sin_demo|titulo=Ecuación de la elipse con los focos en el eje Y|enunciado=*La ecuación de una elipse con semieje mayor <math>a\,</math> y semieje menor <math>b\,</math>, con centro en el origen de coordenadas y focos en el eje de ordenadas es: | + | {{Teorema_sin_demo|titulo=Ecuación de la elipse con los focos en el eje Y|enunciado=:La ecuación de una elipse con semieje mayor <math>a\,</math> y semieje menor <math>b\,</math>, con centro en el origen de coordenadas y focos en el eje de ordenadas es: |
| {{Caja|contenido=<math>\cfrac{x^2}{b^2}+\cfrac{y^2}{a^2}=1</math>}} | {{Caja|contenido=<math>\cfrac{x^2}{b^2}+\cfrac{y^2}{a^2}=1</math>}} | ||
| - | *Su excentricidad es: <math>e=\cfrac{a}{c}</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 195: | Línea 154: | ||
| ===Ecuación de la elipse con el centro desplazado del origen de coordenadas=== | ===Ecuación de la elipse con el centro desplazado del origen de coordenadas=== | ||
| {{Teorema_sin_demo|titulo=Ecuación de la elipse con el centro desplazado del origen|enunciado=:La ecuación de una elipse con semiejes <math>a\,</math> y <math>b\,</math> y centro <math>O(\alpha,\beta)\,</math> es: | {{Teorema_sin_demo|titulo=Ecuación de la elipse con el centro desplazado del origen|enunciado=:La ecuación de una elipse con semiejes <math>a\,</math> y <math>b\,</math> y centro <math>O(\alpha,\beta)\,</math> es: | ||
| - | + | :*Si el eje FF' es paralelo al eje X: | |
| {{Caja|contenido=<math>\cfrac{(x-\alpha)^2}{a^2}+\cfrac{(y-\beta)^2}{b^2}=1</math>}} | {{Caja|contenido=<math>\cfrac{(x-\alpha)^2}{a^2}+\cfrac{(y-\beta)^2}{b^2}=1</math>}} | ||
| - | + | :*Si el eje FF' es perpendicular al eje X: | |
| + | {{Caja|contenido=<math>\cfrac{(x-\alpha)^2}{b^2}+\cfrac{(y-\beta)^2}{a^2}=1</math>}} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Ecuación reducida de la elipse''|cuerpo= | + | {{Video_enlace_julioprofe |
| - | {{ai_cuerpo | + | |titulo1=Ejemplo 1 (parte 1) |
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2. | + | |duracion=9'46" |
| - | + | |sinopsis=Representa gráficamente <math>x^2+4y^2-6x-16y+21=0\;</math>. | |
| - | |actividad=La ecuación reducida viene dada por la fórmula: | + | |url1=https://www.youtube.com/watch?v=849ryoz3LaU |
| + | }} | ||
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{(x-\alpha)^2}{a^2}+\cfrac{(y-\beta)^2}{b^2}=1</math></center> | + | {{Video_enlace_julioprofe |
| + | |titulo1=Ejemplo 1 (parte 2) | ||
| + | |duracion=5'38" | ||
| + | |sinopsis=Representa gráficamente <math>x^2+4y^2-6x-16y+21=0\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=_d1SyjVGVpk | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | Sustituyendo <math>a=5\,</math>, <math>b=2\,</math>, <math>\alpha=3\,</math>, <math>\beta=-1\,</math>, tenemos: | + | {{Geogebra_enlace |
| + | |descripcion=En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2. | ||
| + | |enlace=[https://ggbm.at/zAZPrbmm Ecuación de la elipse con el centro desplazado del origen de coordenadas] | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{(x-3)^2}{25}+\cfrac{(y+1)^2}{4}=1</math></center> | ||
| - | {{p}} | ||
| - | Puedes ver su gráfica en la siguente escena: | ||
| - | <center><iframe> | + | ==Construcciones de la elipse== |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_3.html | + | {{Geogebra_enlace |
| - | width=780 | + | |descripcion=En esta escena podrás ver como construye una elipse por el método del jardinero. Los jardineros, para trazar una forma elíptica sobre la tierra, clavan dos estacas en el suelo, atan entre ambas una cuerda suficientemente amplia y, manteniéndola tensa, trazan una línea sobre la tierra apoyando un palo sobre la cuerda y deslizándolo sobre la misma. |
| - | height=460 | + | |enlace=[https://ggbm.at/f462a5R2 Método del jardinero] |
| - | name=myframe | + | }} |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicio:''' | + | |
| - | #Usando la escena anterior, intenta representar las siguientes elipses y averigua sus parámetros. | + | |
| {{p}} | {{p}} | ||
| - | ::a) <math>\cfrac{(x+2)^2}{16}+\cfrac{(y-3)^2}{25}=1</math> | + | {{Geogebra_enlace |
| - | + | |descripcion=La elipse como envolvente. | |
| - | ::b) <math>x^2+9y^2=9\,</math> | + | |enlace=[https://ggbm.at/Cz2vMk4Y La elipse como envolvente (1)] |
| - | }}}} | + | }} |
| {{p}} | {{p}} | ||
| - | ==Construcciones de la elipse== | + | {{Geogebra_enlace |
| - | {{AI2|titulo=Actividad interactiva: ''Construcciones de la elipse''|cuerpo= | + | |descripcion=La elipse como envolvente. |
| - | {{ai_cuerpo | + | |enlace=[https://ggbm.at/GeRengUD La elipse como envolvente (2)] |
| - | |enunciado='''Actividad 1:''' Método del jardinero. | + | |
| - | |actividad=[[Imagen:trazado_elipse.jpg|right|180px]] Los jardineros, para trazar una forma elíptica sobre la tierra, clavan dos estacas en el suelo, atan entre ambas una cuerda suficientemente amplia y, manteniéndola tensa, trazan una línea sobre la tierra apoyando un palo sobre la cuerda y deslizándolo sobre la misma. | + | |
| - | + | ||
| - | En la siguiente escena, activa la traza, desliza el punto P y observa. | + | |
| - | + | ||
| - | #¿Qué tipo de curva describe la traza de P en su movimiento? | + | |
| - | #¿Qué representan los segmentos morados? | + | |
| - | #¿Qué propiedad cumplen todos los puntos por los que pasa P? | + | |
| - | #¿Qué ocurre si pones c=0? | + | |
| - | + | ||
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_1.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | + | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{p}} |
| - | |enunciado='''Actividad 2:''' La elipse como envolvente (1). | + | {{Geogebra_enlace |
| - | |actividad= | + | |descripcion=La elipse a partir de dos circunferencias. |
| - | + | |enlace=[https://ggbm.at/t8P5SEjD La elipse a partir de dos circunferencias] | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_6.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_6.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa. | + | |
| - | *¿Qué cumple el segmento QR en cada momento respecto al punto F? | + | |
| - | Activa el trazo de QR y vuelve a deslizar el punto Q | + | |
| - | *¿Cuál es la envolvente de la familia de segmentos QR?, es decir, ¿cuál es la curva tangente a esa familia de segmentos? | + | |
| - | Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | + | |
| - | *¿De qué modo influye la posición relativa de F en la forma de la elipse generada? | + | |
| - | + | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{p}} |
| - | |enunciado='''Actividad 3:''' La elipse como envolvente (2). | + | {{Geogebra_enlace |
| - | |actividad= | + | |descripcion=La elipse como hipotrocoide. |
| - | + | |enlace=[https://ggbm.at/UGeNWQU6 La elipse como hipotrocoide] | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_7.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_7.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa. La figura muestra por donde habría de doblarse la cicunferencia (si fuese de papel) para que el punto Q coincidiese con el F. | + | |
| - | + | ||
| - | Activa el trazo de la cuerda y vuelve a deslizar el punto Q | + | |
| - | *¿Cuál es la envolvente de la familia de esas cuerdas?, es decir, ¿cuál es la curva tangente a esa familia de segmentos? | + | |
| - | + | ||
| - | Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | + | |
| - | *¿De qué modo influye la posición relativa de F en la forma de la elipse generada? | + | |
| - | + | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{p}} |
| - | |enunciado='''Actividad 4:''' La elipse a partir de dos circunferencias. | + | {{Geogebra_enlace |
| - | |actividad= | + | |descripcion=La elipse mediante el compás de [[Arquímedes]]. |
| - | + | |enlace=[https://ggbm.at/urzUtA86 La elipse mediante el compás de Arquímedes] | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_8.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_8.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa. | + | |
| - | + | ||
| - | *¿Cómo está determinado el punto P? | + | |
| - | + | ||
| - | Activa su trazo y vuelve a deslizar el punto Q. | + | |
| - | + | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{p}} |
| - | |enunciado='''Actividad 5:''' La elipse como hipotrocoide. | + | {{Geogebra_enlace |
| - | |actividad= | + | |descripcion=La elipse a partir de dos circunferencias tangentes interiores. |
| - | + | |enlace=[https://ggbm.at/Msv3F7D9 La elipse a partir de dos circunferencias tangentes interiores] | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_9.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_9.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto verde y observa. | + | |
| - | + | ||
| }} | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 6:''' La elipse mediante el compás de [[Arquímedes]]. | ||
| - | |actividad= | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_10.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_10.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Al utilizar el deslizador comprobarás el movimiento de un segmento de longitud fija cuyos extremos se deslizan sobre dos ejes perpendiculares. | ||
| - | |||
| - | *¿Qué trayectoria describirá un punto determinado de ese segmento? | ||
| - | |||
| - | Activa el trazo de P para comprobarlo. | ||
| - | |||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 7:''' La elipse a partir de dos circunferencias tangentes interiores. [[Arquímedes]]. | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_11.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_11.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Desliza el punto Q y observa. | ||
| - | |||
| - | Activa el trazo del centro de la circunferencia interior y vuelve a deslizar el punto Q. | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
La elipse
Dados dos puntos 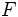 y
y 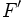 llamados focos, y una distancia
llamados focos, y una distancia  , llamada constante de la elipse (
, llamada constante de la elipse (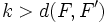 ), se llama elipse al lugar geométrico de los puntos
), se llama elipse al lugar geométrico de los puntos  del plano cuya suma de distancias a los focos es igual a
del plano cuya suma de distancias a los focos es igual a  :
:
|
|
Elementos de la elipse
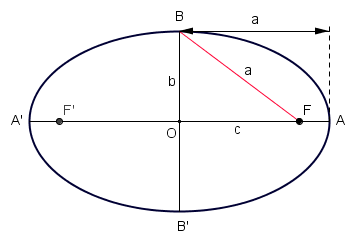
Una elipse de focos
| 
|
Trazado de una elipse y elementos principales.
En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco.
Excentricidad de la elipse
La excentricidad de la elipse es el cociente entre la distancia focal y el eje mayor:
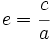
Propiedades
- En una elipse
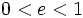 .
.
- Una elipse más se parece a a una circunferencia, cuanto más se aproxime a 0 su excentricidad.
- Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que

- y como
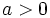 y
y  , tenemos que
, tenemos que 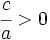
- Cuanto más próxima a 0 sea la excentricidad, más proximo a cero estará
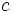 (la distancia focal se aproximará a cero) y
(la distancia focal se aproximará a cero) y  se aproximará a
se aproximará a  . Así, la elipse, se aproximará a una circunferencia de centro los focos y radio
. Así, la elipse, se aproximará a una circunferencia de centro los focos y radio 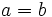 .
.
En la siguiente escena vamos a ver como se ve afectada la elipse si modificamos su excentricidad.
Ecuaciones de la elipse
Ecuación reducida de la elipse
Ecuación reducida de la elipse
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y 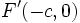 los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
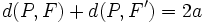
Sustituyendo las distancias por su fórmula matemática:
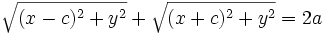
Pasamos la segunda raíz al segundo miembro:
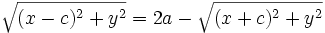
Se elevan al cuadrado ambos miebros y se simplifica:
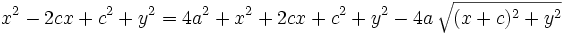
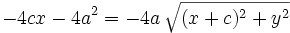
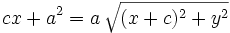
Se elevan al cuadrado los dos miembros:
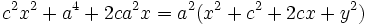
Reordenando y agrupando términos:
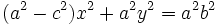
Teniendo en cuenta que 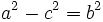 :
:
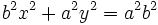
Dividiendo la expresión por 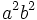 :
:
se obtiene la cuación buscada:
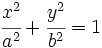
Ecuación reducida de la elipse de eje mayor 40 y distancia focal 24
En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9.
Ecuación de la elipse con los focos en el eje Y
Ecuación de la elipse con los focos en el eje Y
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
Ecuación de la elipse con el centro desplazado del origen de coordenadas
Ecuación de la elipse con el centro desplazado del origen
- La ecuación de una elipse con semiejes
 y
y  y centro
y centro 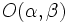 es:
es:
- Si el eje FF' es paralelo al eje X:
|
|
- Si el eje FF' es perpendicular al eje X:
|
|
Representa gráficamente 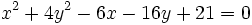 .
.
Representa gráficamente 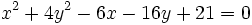 .
.
En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2.
Construcciones de la elipse
En esta escena podrás ver como construye una elipse por el método del jardinero. Los jardineros, para trazar una forma elíptica sobre la tierra, clavan dos estacas en el suelo, atan entre ambas una cuerda suficientemente amplia y, manteniéndola tensa, trazan una línea sobre la tierra apoyando un palo sobre la cuerda y deslizándolo sobre la misma.
La elipse como envolvente.
La elipse como envolvente.
La elipse a partir de dos circunferencias.
La elipse como hipotrocoide.
La elipse mediante el compás de Arquímedes.
La elipse a partir de dos circunferencias tangentes interiores.
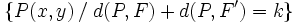
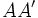 y
y 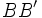 , que se cortan en el centro
, que se cortan en el centro  de la elipse, determina los siguientes segmentos:
de la elipse, determina los siguientes segmentos:
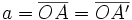
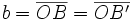
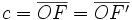
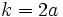 (constante de la elipse)
(constante de la elipse)
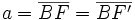
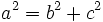
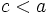
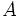 un punto de la elipse:
un punto de la elipse:
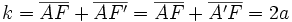
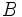 un punto de la elipse:
un punto de la elipse:
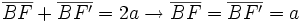
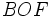 , tenemos
, tenemos