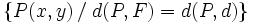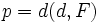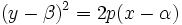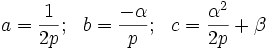La parábola (1ºBach)
De Wikipedia
| Revisión de 08:16 24 abr 2017 Coordinador (Discusión | contribuciones) (→Ecuación de la parábola con el vértice desplazado del origen de coordenadas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 106: | Línea 106: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ecuación de la parábola. | ||
| - | |duracion=10'29" | ||
| - | |sinopsis=Ecuación de la parábola. | ||
| - | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/conicas/parabola/parabola-01 | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| ===Ecuación de la parábola con eje de simetría vertical=== | ===Ecuación de la parábola con eje de simetría vertical=== | ||
| {{Teorema_sin_demo|titulo=Ecuación de la parábola con eje de simetría vertical|enunciado=:La ecuación de una parábola con directriz paralela al eje de abscisas y vértice en el el punto <math>O(\alpha,\beta)\,</math>, es: | {{Teorema_sin_demo|titulo=Ecuación de la parábola con eje de simetría vertical|enunciado=:La ecuación de una parábola con directriz paralela al eje de abscisas y vértice en el el punto <math>O(\alpha,\beta)\,</math>, es: | ||
| Línea 161: | Línea 153: | ||
| }} | }} | ||
| - | + | {{p}} | |
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Parábolas con ejes verticales y horizontales. | ||
| + | |duracion=10'29" | ||
| + | |sinopsis=Parábolas con ejes verticales y horizontales. Ejemplo | ||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/conicas/parabola/parabola-01 | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 1 | ||
| + | |duracion=8'21" | ||
| + | |sinopsis=Construir la parábola con vértice (3,2) y foco (3,4). Halla su ecuación estandard y su ecuación general. | ||
| + | |url1=https://www.youtube.com/watch?v=N8WhvRJbGC8 | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 2 | ||
| + | |duracion=9'44" | ||
| + | |sinopsis=Halla el vértice y el foco de la parábola de ecuación general <math>2x^2+8x-y+8=0</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=2pvke2ELR3M | ||
| + | }} | ||
| + | {{p}} | ||
| ==Construcciones de la parábola== | ==Construcciones de la parábola== | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
La parábola
Dados un punto
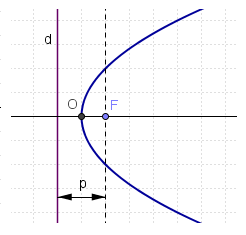
[editar] Elementos de la parábolaUna parábola de foco
| 
|
Escena que muestra la propiedad de la parábola de que cualquier "rayo" perpendicular a la directriz rebota en la tangente a la curva y se refleja en dirección al foco.
Aplicaciones prácticas:
- Las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
- La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
- Analogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal.
En la siguiente escena vamos a estudiar la trayectoria de un proyectil.
Excentricidad de la parábola
La excentricidad de la parábola es el cociente entre 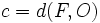 y
y 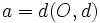 . En consecuencia, la excentricidad de la parábola es siempre igual a 1.
. En consecuencia, la excentricidad de la parábola es siempre igual a 1.
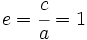
Ecuaciones de la parábola
Ecuación reducida de la parábola
Ecuación reducida de la parábola
- La ecuación de una parábola con foco en el eje de abscisas, directriz paralela al eje de ordenadas y vértice en el origen de coordenadas, es:
|
|
Recordemos que 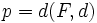 . Por tanto, las coordenadas del foco y la ecuación de la directiz son:
. Por tanto, las coordenadas del foco y la ecuación de la directiz son:
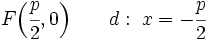
Como cualquier punto  de la parábola cumple que:
de la parábola cumple que:
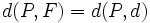
Sustituyendo las distancias por su fórmula matemática, tenemos:
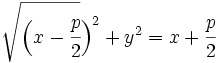
Elevando ambos miembros al cuadrado:
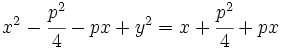
Y simplificando:
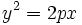
En la siguiente escena vamos a calcular la ecuación reducida de la parábola con distancia del foco a la directriz p=2.
Ecuación de la parábola con el vértice desplazado del origen de coordenadas
Ecuación de la parábola con el vértice desplazado del origen de coordenadas
- La ecuación de una parábola con directriz paralela al eje de ordenadas y vértice en el el punto
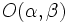 , es:
, es:
|
|
Ecuación de la parábola con eje de simetría vertical
Ecuación de la parábola con eje de simetría vertical
- La ecuación de una parábola con directriz paralela al eje de abscisas y vértice en el el punto
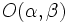 , es:
, es:
|
|
Esta ecuación también se puede expresar de la siguiente manera:
Ecuación de la parábola con eje de simetría vertical
- La ecuación de una parábola con directriz paralela al eje de abscisas y vértice en el el punto
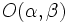 , es:
, es:
|
|
donde
Basta con desarrollar la ecuación
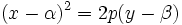

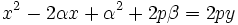
Despejando 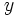 :
:
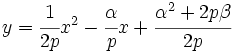
donde basta con llamar:
Proposición
- Las coordenadas vértice
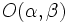 , de una parábola con directriz paralela al eje de abscisas
, de una parábola con directriz paralela al eje de abscisas 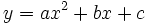 , son:
, son:

Partiendo del resultado anterior en el que teníamos que:
Despejando 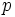 de la primera ecuación:
de la primera ecuación: 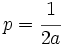
Despejando  de la segunda ecuación:
de la segunda ecuación: 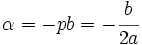
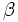 de la tercera ecuación:
de la tercera ecuación: 
Parábolas con ejes verticales y horizontales. Ejemplo
Construir la parábola con vértice (3,2) y foco (3,4). Halla su ecuación estandard y su ecuación general.
Halla el vértice y el foco de la parábola de ecuación general 2x2 + 8x − y + 8 = 0.
Construcciones de la parábola
Método de construcción de la parábola basado en su definición como lugar geométrico.
Construcción de la parábola como envolvente.
Generación de la parábola a partir del centro de una circunferencia.
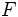 llamado foco, y una recta
llamado foco, y una recta 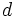 , llamada directriz, se llama parábola al lugar geométrico de los puntos
, llamada directriz, se llama parábola al lugar geométrico de los puntos  del plano que equidistán del foco y de la directriz:
del plano que equidistán del foco y de la directriz: