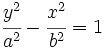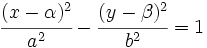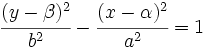La hipérbola (1ºBach)
De Wikipedia
| Revisión de 16:43 20 oct 2016 Coordinador (Discusión | contribuciones) (→Ecuación reducida de la hipérbola) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ecuación de la hipérbola con el centro desplazado del origen de coordenadas) |
||
| Línea 137: | Línea 137: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Ecuación de la hipérbola con el centro desplazado del origen de coordenadas''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=En la siguiente escena vamos a calcular la ecuación de la hipérbola de centro O(-3,1), semieje a=3 y semidistancia focal c=5. |
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a calcular la ecuación de la hipérbola de centro O(-3,1), semieje a=3 y semidistancia focal c=5. | + | |enlace=[https://ggbm.at/WJxFDtKT Ecuación de la hipérbola con el centro desplazado del origen de coordenadas] |
| - | + | }} | |
| - | |actividad=La ecuación viene dada por la fórmula: | + | |
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{(x-\alpha)^2}{a^2}-\cfrac{(y-\beta)^2}{b^2}=1</math></center> | + | {{Geogebra_enlace |
| - | + | |descripcion=En la siguiente escena vamos a calcular la ecuación de la hipérbola con eje focal vertical de centro O(3,-1), a=2 y b=3. | |
| - | + | |enlace=[https://ggbm.at/KYXPc5Uz Ecuación de la hipérbola con el eje vertical] | |
| - | Sustituyendo: {{sube|porcentaje=15%|contenido=<math>a=3 \, , \quad b=\sqrt{c^2-a^2}=\sqrt{5^2-3^2}=4\, , \quad \alpha=-3\, , \quad \beta=1\,</math>}}, tenemos: | + | }} |
| - | + | ||
| - | + | ||
| - | <center><math>\cfrac{(x+3)^2}{9}-\cfrac{(y-1)^2}{16}=1</math></center> | + | |
| {{p}} | {{p}} | ||
| - | Puedes ver su gráfica en la siguente escena: | + | {{Video_enlace_julioprofe |
| - | + | |titulo1=Ejemplo 1 (parte 1) | |
| - | <center><iframe> | + | |duracion=9'32" |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_3.html | + | |sinopsis=Representa la cónica de ecuación general <math>9x^2-16y^2-108x+128y+212=0</math>. |
| - | width=780 | + | |url1=https://www.youtube.com/watch?v=zMDjlUlArqI |
| - | height=460 | + | }} |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicio:''' | + | |
| - | #Usando la escena anterior, intenta representar las siguientes elipses y averigua sus parámetros. | + | |
| {{p}} | {{p}} | ||
| - | ::a) <math>\cfrac{(x-4)^2}{25}+\cfrac{(y+1)^2}{4}=1</math> | ||
| - | ::b) <math>4x^2-y^2=4\,</math> | + | {{Video_enlace_julioprofe |
| + | |titulo1=Ejemplo 1 (parte 2) | ||
| + | |duracion=9'52" | ||
| + | |sinopsis=Representa la cónica de ecuación general <math>9x^2-16y^2-108x+128y+212=0</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=6jP3VRiEa-o | ||
| }} | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2''' En la siguiente escena vamos a calcular la ecuación de la hipérbola con eje focal vertical de centro O(3,-1), a=2 y b=3. | ||
| - | |||
| - | |actividad=La ecuación viene dada por la fórmula: | ||
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{(y-\beta)^2}{b^2}-\cfrac{(x-\alpha)^2}{a^2}=1</math></center> | + | {{Video_enlace_unicoos |
| - | + | |titulo1=Ejemplo 2 | |
| - | + | |duracion=16'15" | |
| - | Sustituyendo: {{sube|porcentaje=10%|contenido=<math>a=2 \, , \quad b=3\, , \quad \alpha=3\, , \quad \beta=-1\,</math>}}, tenemos: | + | |sinopsis=Representa gráficamente la hipérbola de ecuación <math>4x^2-3y^2-8x-8=0</math>. |
| - | + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/conicas/hiperbola/hiperbola-no-centrada-en-el-origen | |
| - | + | }} | |
| - | <center><math>\cfrac{(y+1)^2}{9}-\cfrac{(x-3)^2}{4}=1</math></center> | + | |
| {{p}} | {{p}} | ||
| - | Puedes ver su gráfica en la siguente escena: | ||
| - | <center><iframe> | + | ==Construcciones de la hipérbola== |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_5.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_5.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | '''Ejercicio:''' | + | |
| - | #Usando la escena anterior, intenta representar las siguientes elipses y averigua sus parámetros. | + | |
| {{p}} | {{p}} | ||
| - | ::a) <math>\cfrac{(y-1)^2}{4}+\cfrac{(x-2)^2}{16}=1</math> | + | {{Geogebra_enlace |
| - | + | |descripcion=En esta escena podrás ver como construye una hipérbola usando la definición de hipérbola como lugar geométrico. | |
| - | ::b) <math>y^2-x^2=1\,</math> | + | |enlace=[https://ggbm.at/ukt4c5TW Trazado de la hipérbola a partir de la definición] |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | + | {{Geogebra_enlace | |
| - | ==Construcciones de la hipérbola== | + | |descripcion=En esta escena podrás ver como construye una hipérbola como envolvente. |
| - | {{AI2|titulo=Actividad interactiva: ''Construcciones de la hipérbola''|cuerpo= | + | |enlace=[https://ggbm.at/d8srPsgC La hipérbola como envolvente] |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1:''' Usando la definición de hipérbola como lugar geométrico. | + | |
| - | |actividad= | + | |
| - | En la siguiente escena, activa la traza, desliza el punto P y observa. | + | |
| - | + | ||
| - | *¿Qué tipo de curva describe la traza de P en su movimiento? | + | |
| - | *¿Qué representan los segmentos verde y morado? | + | |
| - | *¿Qué propiedad cumplen todos los puntos por los que pasa P? | + | |
| - | *Desliza ahora el punto P' | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_1.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2:''' La hipérbola como envolvente. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_6.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_6.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Desliza el punto Q y observa los cambios. | + | |
| - | + | ||
| - | Activa el trazo de la recta y vuelve a deslizar Q | + | |
| - | + | ||
| - | *Aparece una hipérbola como la envolvente ¿de qué familia de rectas? | + | |
| - | + | ||
| - | Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior. | + | |
| - | + | ||
| - | *¿De qué modo influye la posición relativa de F en la forma de la cónica generada? | + | |
| - | + | ||
| - | }} | + | |
| - | + | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
La hipérbola
Dados dos puntos 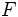 y
y 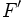 llamados focos, y una distancia
llamados focos, y una distancia  , llamada constante de la hipérbola (
, llamada constante de la hipérbola (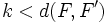 ), se llama hipérbola al lugar geométrico de los puntos
), se llama hipérbola al lugar geométrico de los puntos  del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a
del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a  :
:
|
|
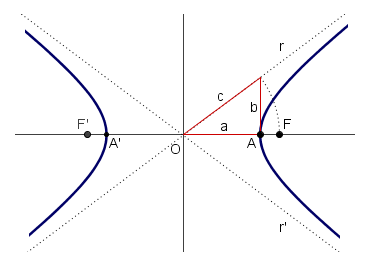
Elementos de la hipérbola
Una una hipérbola de focos
Propiedades
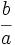 y y 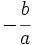 Demostración:
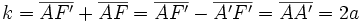
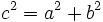 Por ser
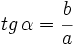 |
Excentricidad de la hipérbola
La excentricidad de la hipérbola es el cociente entre la distancia focal y el eje:
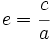
Propiedades
En una hipérbola 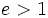 .
.
Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que
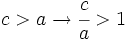
En la siguiente escena vamos a ver como se ve afectada la hipérbola si modificamos su excentricidad.
Ecuaciones de la hipérbola
Ecuación reducida de la hipérbola
Ecuación reducida de la hipérbola
- La ecuación de una hipérbola con semieje
 , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y 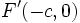 los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
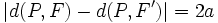
Sustituyendo las distancias por su fórmula matemática, y contemplando la posibilidad del doble signo que surge de suprimir el valor absoluto:
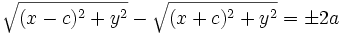
Pasamos la segunda raíz al segundo miembro:
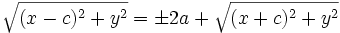
Se elevan al cuadrado ambos miebros y se simplifica:
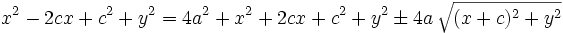
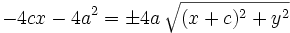
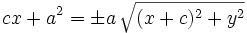
Se elevan al cuadrado los dos miembros:
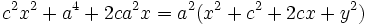
Reordenando y agrupando términos:
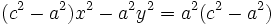
Teniendo en cuenta que 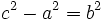 :
:
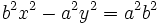
Dividiendo la expresión por 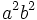 :
:
se obtiene la cuación buscada:
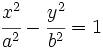
En la siguiente escena vamos a calcular la ecuación reducida de la hipérbola con semieje 4 y semidistancia focal 5.
Ecuación de la hipérbola con los focos en el eje Y
Ecuación de la hipérbola con los focos en el eje Y
- La ecuación de una hipérbola con semieje
 , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
Ecuación de la hipérbola con el centro desplazado del origen de coordenadas
Ecuación de la hipérbola con el centro desplazado del origen
- La ecuación de una elipse con semieje
 y centro
y centro 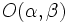 es:
es:
- Si el eje FF' es paralelo al eje X:
|
|
- Si el eje FF' es perpendicular al eje X:
|
|
En la siguiente escena vamos a calcular la ecuación de la hipérbola de centro O(-3,1), semieje a=3 y semidistancia focal c=5.
En la siguiente escena vamos a calcular la ecuación de la hipérbola con eje focal vertical de centro O(3,-1), a=2 y b=3.
Representa la cónica de ecuación general 9x2 − 16y2 − 108x + 128y + 212 = 0.
Representa la cónica de ecuación general 9x2 − 16y2 − 108x + 128y + 212 = 0.
Representa gráficamente la hipérbola de ecuación 4x2 − 3y2 − 8x − 8 = 0.
Construcciones de la hipérbola
En esta escena podrás ver como construye una hipérbola usando la definición de hipérbola como lugar geométrico.
En esta escena podrás ver como construye una hipérbola como envolvente.
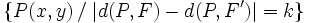
 y
y 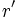
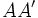

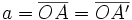
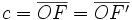
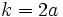 (constante de la hipérbola)
(constante de la hipérbola)
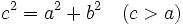
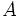 un punto de la hipérbola:
un punto de la hipérbola:
 y
y 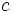 , tenemos
, tenemos
 .
.