Plantilla:Máximo común divisor
De Wikipedia
| Revisión de 19:11 3 may 2017 Coordinador (Discusión | contribuciones) (→Números primos entre sí) ← Ir a diferencia anterior |
Revisión de 09:35 11 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplos | + | |titulo1=Ejemplos 1 |
| + | |duracion=5'52" | ||
| + | |sinopsis=Cálculo del máximo común divisor. Ejemplos | ||
| + | |url1=https://www.youtube.com/watch?v=m3pRyjadWgI}} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplos 1 | ||
| |duracion=14'59" | |duracion=14'59" | ||
| |sinopsis=Concepto de máximo común divisor. Ejemplos usando los dos métodos. | |sinopsis=Concepto de máximo común divisor. Ejemplos usando los dos métodos. | ||
Revisión de 09:35 11 may 2017
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Cálculo del máximo común divisor
- Para obtenerlo se descomponen los números en factores primos y se toman los factores comunes elevados al menor exponente.
- Calcula el m.c.d.(24,60).
- Primer método:
- Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
- Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- m.c.d.(24,60)= 12
- Segundo método:
- Descomponemos 24 y 60 en sus factores primos:
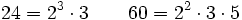
- Multiplicando los factores comunes elevados al menor exponente:
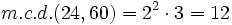
Ejemplos 1 (5'52") Sinopsis: Cálculo del máximo común divisor. Ejemplos
Ejemplos 1 (14'59") Sinopsis: Concepto de máximo común divisor. Ejemplos usando los dos métodos.
Propiedades
Propiedad
- Si a es múltiplo de b, entonces m.c.d.(a,b)=b.
- m.c.d.(15, 30)=15, porque 30 es múltiplo de 15.
Números primos entre sí
Dos números son primos entre sí, si su m.c.d. es 1.
- 6 y 11 son primos entre sí.
Propiedades
Si a y b son primos entre sí, entonces m.c.m.(a,b)=a · b.
- Como 6 y 11 son primos entre sí, entonces m.c.m(6,11)=6·11=66
Actividades
Calcula el m.c.d. de dos números Descripción: Calcula mentalmente y anota en tu cuaderno el máximo común divisor de estos dos números; márcalo en la ventana del control inferior y pulsa intro.
Si necesitas ayuda pulsa sobre los triángulos del control de arriba y verás la descomposición factorial de cada número, pero en ese caso el mensaje ENHORABUENA tendrá otro color.
Cada vez que pulses sobre "inicio" aparecerán otros dos números aleatoriamente.
Actividad: Máximo común divisor
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio resuelto: m.c.d.
En un almacén quieren envasar, para su distribución, 200 kg de manzanas y 260 kg de de naranjas, en cajones del mismo peso y de la mayor carga que sea posible. ¿Cuántos kilos deben poner en cada cajón?
- Solucuión: 20 kg
