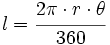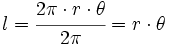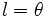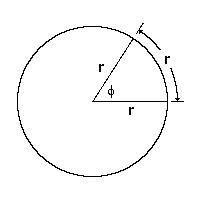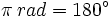Medida de ángulos: el radián (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:33 15 may 2017 Coordinador (Discusión | contribuciones) (→El radián) ← Ir a diferencia anterior |
Revisión de 08:34 15 may 2017 Coordinador (Discusión | contribuciones) (→Equivalencia entre radianes y grados sexagesimales) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| ==Equivalencia entre radianes y grados sexagesimales== | ==Equivalencia entre radianes y grados sexagesimales== | ||
| - | {{Teorema | + | {{Equivalencia entre radianes y grados sexagesimales}} |
| - | |titulo=Equivalencia entre radianes y grados sexagesimales | + | |
| - | |enunciado={{Caja|contenido=<math> \pi \, rad = 180^\circ</math>}} | + | |
| - | {{p}} | + | |
| - | En consecuencia: | + | |
| - | <center><math>1 \, rad=\cfrac{180^\circ}{\pi} \approx 57^\circ 17' 45 '' \qquad \qquad1^\circ = \cfrac {\pi \, rad} {180} \approx 0.0175 \, rad</math></center> | + | |
| - | |demo=Como la longitud de una circunferencia de radio <math>R \,</math> es <math>2 \pi R \,</math>, tenemos que una circunferencia contiene <math>2 \pi \,</math> veces a la radio. Por tanto, 360º equivalen a <math>2 \pi \,</math> rad y , dividiendo por 2, 180º equivalen a <math>\pi \,</math> rad. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | Utilizando la equivalencia anterior, y mediante una regla de tres, podemos obtener las siguientes equivalencias: | + | |
| - | <br> | + | |
| - | + | ||
| - | {|align=center border=1 cellpadding=4 cellspacing=0 | + | |
| - | |- valign="top" | + | |
| - | |style = "background:#f2f2f2" | '''Grados''' | + | |
| - | |style = "width:3em; text-align:center" | 0° | + | |
| - | |style = "width:3em; text-align:center" | 30° | + | |
| - | |style = "width:3em; text-align:center" | 45° | + | |
| - | |style = "width:3em; text-align:center" | 60° | + | |
| - | |style = "width:3em; text-align:center" | 90° | + | |
| - | |style = "width:3em; text-align:center" | 180° | + | |
| - | |style = "width:3em; text-align:center" | 270° | + | |
| - | |style = "width:3em; text-align:center" | 360° | + | |
| - | |- valign="top" | + | |
| - | |style = "background:#f2f2f2" | '''Radianes''' | + | |
| - | |style = "text-align:center" | 0 | + | |
| - | |style = "text-align:center" | π/6 | + | |
| - | |style = "text-align:center" | π/4 | + | |
| - | |style = "text-align:center" | π/3 | + | |
| - | |style = "text-align:center" | π/2 | + | |
| - | |style = "text-align:center" | π | + | |
| - | |style = "text-align:center" | 3π/2 | + | |
| - | |style = "text-align:center" | 2π | + | |
| - | |} | + | |
| - | {{p}} | + | |
| - | {{wolfram desplegable|titulo=El radian|contenido= | + | |
| - | {{wolfram | + | |
| - | |titulo=Actividad: ''El radian'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | + | ||
| - | :a) Convierte 300º en radianes. | + | |
| - | :b) Convierte 3 rad en grados sexagesimales. | + | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) {{consulta|texto=convert 300º to radians}} | + | |
| - | :b) {{consulta|texto=convert 3 rad to degrees}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| - | + | ||
| {{Videotutoriales|titulo=Medida de ángulos.|enunciado= | {{Videotutoriales|titulo=Medida de ángulos.|enunciado= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
Revisión de 08:34 15 may 2017
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
El radián
Equivalencia entre radianes y grados sexagesimales
Equivalencia entre radianes y grados sexagesimales
|
|
En consecuencia:

Demostración:
Como la longitud de una circunferencia de radio
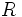 es
es 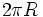 , tenemos que una circunferencia contiene
, tenemos que una circunferencia contiene 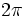 veces a la radio. Por tanto, 360º equivalen a
veces a la radio. Por tanto, 360º equivalen a 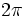 rad y , dividiendo por 2, 180º equivalen a
rad y , dividiendo por 2, 180º equivalen a 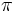 rad.
rad.Utilizando la equivalencia anterior, y mediante una regla de tres, podemos obtener las siguientes equivalencias:
| Grados | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
- Definición de ángulo. Tipos.
- Sistema sexagesimal.
- Definición de radian.
- Equivalencia entre radianes y grados sexagesimales
- Expresa el ángulo 32,56º (32 grados y 56 centésimas de grado) en grados, minutos y segundos.
- Expresa el ángulo 46º15'36" en grados sexagesimales.
- Expresa el ángulo 2,6 rad. en grados, minutos y segundos.
- Expresa en radianes el ángulo 72º.
Expresa 750º en radianes.
Expresa 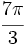 radianes en grados.
radianes en grados.
Calculadora
|
Calculadora: Pasar ángulos con formato decimal a formato "grados, minutos y segundos" y viceversa |
Ejercicios propuestos
|
Ejercicios propuestos: El radián |
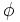 mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.