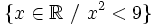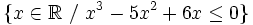Plantilla:Intervalos y semirrectas
De Wikipedia
| Revisión de 09:01 7 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:00 20 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| |La '''recta real''' se representa en forma de intervalo: <math> \mathbb{R}=( - \infty, + \infty )</math> | |La '''recta real''' se representa en forma de intervalo: <math> \mathbb{R}=( - \infty, + \infty )</math> | ||
| |} | |} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Intervalos de la recta real | ||
| + | |duracion=7'06" | ||
| + | |sinopsis=En este vídeo introducimos los conceptos de intervalo abierto (a;b), intervalo cerrado [a;b], intervalo abierto por la izquierda y cerrado por la derecha (a;b], intervalo cerrado por la izquierda y abierto por la derecha [a;b). | ||
| + | También hablamos de la amplitud de un intervalo y de los intervalos de amplitud infinita, llamados "no acotados". | ||
| + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/07-intervalos-de-la-recta-real-6#.VCVY6xZ8HA8 | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| Línea 29: | Línea 37: | ||
| |enlace=[https://ggbm.at/y7UeF9hG Desigualdades] | |enlace=[https://ggbm.at/y7UeF9hG Desigualdades] | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Autoevaluación sobre la interpretación gráfica del conjunto solución de una desigualdad. | |descripcion=Autoevaluación sobre la interpretación gráfica del conjunto solución de una desigualdad. | ||
| |enlace=[https://ggbm.at/D9vjwstx Autoevaluación: Desigualdades] | |enlace=[https://ggbm.at/D9vjwstx Autoevaluación: Desigualdades] | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Expresión de conjuntos numéricos en forma de intervalos. | |descripcion=Expresión de conjuntos numéricos en forma de intervalos. | ||
| |enlace=[https://ggbm.at/MpnWEj6X Intervalos I] | |enlace=[https://ggbm.at/MpnWEj6X Intervalos I] | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos. | |descripcion=Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos. | ||
| |enlace=[https://ggbm.at/VhcRJac5 Autoevaluación: Intervalos I] | |enlace=[https://ggbm.at/VhcRJac5 Autoevaluación: Intervalos I] | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Expresión de conjuntos numéricos en forma de intervalos. | |descripcion=Expresión de conjuntos numéricos en forma de intervalos. | ||
| |enlace=[https://ggbm.at/MfCr2HHt Intervalos II] | |enlace=[https://ggbm.at/MfCr2HHt Intervalos II] | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos. | |descripcion=Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos. | ||
| |enlace=[https://ggbm.at/Y84SqZzh Autoevaluación: Intervalos II] | |enlace=[https://ggbm.at/Y84SqZzh Autoevaluación: Intervalos II] | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Intervalos de la recta real | ||
| - | |duracion=7'06" | ||
| - | |sinopsis=En este vídeo introducimos los conceptos de intervalo abierto (a;b), intervalo cerrado [a;b], intervalo abierto por la izquierda y cerrado por la derecha (a;b], intervalo cerrado por la izquierda y abierto por la derecha [a;b). | ||
| - | También hablamos de la amplitud de un intervalo y de los intervalos de amplitud infinita, llamados "no acotados". | ||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/07-intervalos-de-la-recta-real-6#.VCVY6xZ8HA8 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 08:00 20 may 2017
Para designar algunos tramos de la recta real, existe una nomenclatura que debes conocer:
La recta real se representa en forma de intervalo: 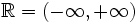
|
En este vídeo introducimos los conceptos de intervalo abierto (a;b), intervalo cerrado [a;b], intervalo abierto por la izquierda y cerrado por la derecha (a;b], intervalo cerrado por la izquierda y abierto por la derecha [a;b). También hablamos de la amplitud de un intervalo y de los intervalos de amplitud infinita, llamados "no acotados".
Interpretación gráfica del conjunto solución de una desigualdad.
Autoevaluación sobre la interpretación gráfica del conjunto solución de una desigualdad.
Expresión de conjuntos numéricos en forma de intervalos.
Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos.
Expresión de conjuntos numéricos en forma de intervalos.
Autoevaluación sobre la expresión de conjuntos numéricos en forma de intervalos.
Ejercicios resueltos: Intervalos y semirrectas
1. Representar los siguientes conjuntos numéricos:
- a) Números mayores que 3.
- b)
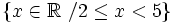
- c)
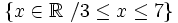
- d) Números menores que 1 excluyendo el 0.
- e)
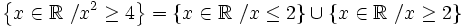
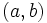
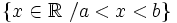
![[a, b]\,\!](/wikipedia/images/math/8/b/5/8b596d04e319e05cadcc7dcf251a9815.png)
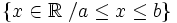
![(a, b]\,\!](/wikipedia/images/math/e/4/5/e4598ac5b1b1c763827cd6adf382190b.png)
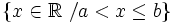
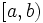
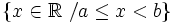
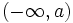
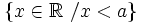
![( - \infty , a]\,\!](/wikipedia/images/math/a/5/3/a537d0975ab601b18b2e6f48b6700575.png)
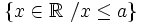
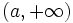
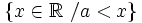
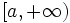
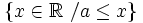
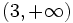
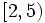
![[ 3, 7 ]\;](/wikipedia/images/math/5/2/5/525d3facf3fc1d833da47b47559cbd4a.png)
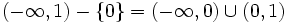
![( -\infty, -2 ] \cup [ 2 , +\infty ]](/wikipedia/images/math/8/7/c/87c992202512c1d40eb658f6c4171c9a.png)

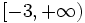
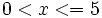
![(-\infty,7],\ [-8,9),\ [-4,7] \;](/wikipedia/images/math/6/f/c/6fcf1a640e06f181cdd7f64424e1953a.png)