Plantilla:Teorema del resto
De Wikipedia
| Revisión de 20:05 20 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:06 20 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 41: | Línea 41: | ||
| *Como ejemplo, también resolveremos los siguientes ejercicios: | *Como ejemplo, también resolveremos los siguientes ejercicios: | ||
| - | :1) Halla el resto de dividir el polinomio <math>2x^4-5x^3+3x-6\;</math> entre el binomio <math>(x-2)\;</math>. | + | :1) Halla el resto de dividir el polinomio <math>2x^4-5x^3+3x-6\;</math> entre el binomio <math>x-2\;</math>. |
| - | :2) Halla el resto de dividir el polinomio <math>9x^3+3x^2+3x+1\;</math> entre el binomio <math>(3x+1)\;</math>. | + | :2) Halla el resto de dividir el polinomio <math>9x^3+3x^2+3x+1\;</math> entre el binomio <math>3x+1\;</math>. |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplos 2 | + | |titulo1=Ejemplo |
| |duracion=3'33" | |duracion=3'33" | ||
| |sinopsis=Halla el resto de la división del polinomio <math>x^3-2x^2+9\;</math> entre <math>x+2\;</math>. | |sinopsis=Halla el resto de la división del polinomio <math>x^3-2x^2+9\;</math> entre <math>x+2\;</math>. | ||
Revisión de 20:06 20 may 2017
Teorema del Resto
El valor que toma un polinomio,  , cuando hacemos
, cuando hacemos  , coincide con el resto de la división de
, coincide con el resto de la división de  entre
entre 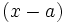 . Es decir,
. Es decir, 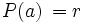 , donde
, donde  es el resto de dicha división.
es el resto de dicha división.
Esto se deduce directamente de una de las propiedades de la división, la que dice que:
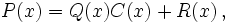
donde  es el dividendo,
es el dividendo,  el divisor,
el divisor, 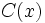 el cociente y
el cociente y 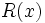 el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de 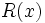 es menor que el grado de
es menor que el grado de  .
.
En efecto, si tomamos el divisor 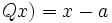 , entonces
, entonces 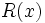 tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar  , y la fórmula anterior se convierte en:
, y la fórmula anterior se convierte en:
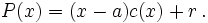
Tomando el valor 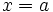 se obtiene que:
se obtiene que:
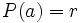
Ejemplo: Teorema del Resto
Calcula el resto de dividir el polinomio 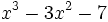 entre
entre 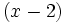
Bastará calcular 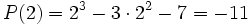
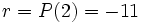
Si P(x) es un polinomio de grado no inferior a 1, el resto de la división P(x)/(x-a) es el número P(a) que se obtiene al sustituir "x" por "a" en P(x). La división P(x)/(x-a) es "exacta" si P(a) = 0; y en tal caso se dice que "a" es un "cero" o "raíz" del polinomio P(x), o una solución de la ecuación P(x) = 0.
- En este vídeo se explica la aplicación del teorema del resto en la división de polinomios.
- Como ejemplo, también resolveremos los siguientes ejercicios:
- 1) Halla el resto de dividir el polinomio
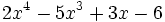 entre el binomio
entre el binomio 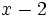 .
.
- 2) Halla el resto de dividir el polinomio
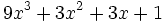 entre el binomio
entre el binomio 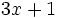 .
.
Halla el resto de la división del polinomio 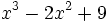 entre
entre 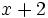 .
.
Halla el valor de  para que la división del polinomio
para que la división del polinomio 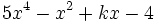 entre
entre 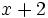 sea exacta.
sea exacta.
Videotutorial.

