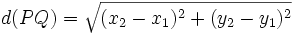Plantilla:Cálculo de la distancia entre dos puntos

De Wikipedia

(Diferencia entre revisiones)

Revisión actual

Conocidas las coordenadas de dos puntos del plano, el teorema de Pitágoras nos permite calcular la distancia entre ambos:

Proposición

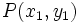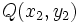La distancia entre dos puntos $P(x_1,y_1)\,$ y $Q(x_2,y_2)\,$ es igual a:

$d(PQ)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Demostración:

Demostración:

Ver el siguiente videotutorial.

Distancia ente dos puntos

Tutorial 1 (8´59") Sinopsis:

Módulo de un vector = distancia entre dos puntos. Demostración de la fórmula.
Ejemplos y ejercicios.

Tutorial 2 (8'37") Sinopsis:

Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.

Tutorial 3 (6'12") Sinopsis:

Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.

Tutorial 4 (10'06") Sinopsis:

Fórmula de la distancia euclidea entre dos puntos del plano. Ejemplos.
Otra distancia: la "distancia de Manhattan".

Cálculo de distancias:

Ejercicio 1 (2'30") Sinopsis:

Halla la distancia entre los puntos A(7,3) y B(3,-1).

Ejercicio 2 (4'17") Sinopsis:

Halla la distancia entre los puntos A(3,1/2) y B(4/3,-1).

Ejercicio 3 (4'21") Sinopsis:

Halla la distancia entre los puntos A(3/2,-1/6) y B(-1/2,1/3).

Ejercicio 4 (3'31") Sinopsis:

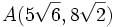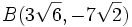Halla la distancia entre los puntos $A(5\sqrt{6},8\sqrt{2})\;$ y $B(3\sqrt{6},-7\sqrt{2})\;$ .

Ejercicio 5 (4'49") Sinopsis:

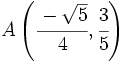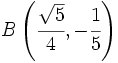Halla la distancia entre los puntos $A \left( \cfrac{-\sqrt{5}}{4},\cfrac{3}{5}\right)\;$ y $B \left(\cfrac{\sqrt{5}}{4},-\cfrac{1}{5}\right)\;$ .

Halla la coordenada que falta:

Ejercicio 1 (5'11") Sinopsis:

Halla el valor de "x" para que la distancia entre los puntos A(x,-1) y B(9,4) sea 13.

Ejercicio 2 (4'30") Sinopsis:

Halla el valor de "y" para que la distancia entre los puntos P(7,1) y Q(3,y) sea 5.

Ejercicio 3 (6'09") Sinopsis:

Halla el punto Q el eje Y que equidista de A(4,2) y B(5,5).

Ejercicio 4 (5'26") Sinopsis:

Halla el punto P el eje X que equidista de A(5,1) y B(0,6).

Ejercicio 5 (11'53") Sinopsis:

Halla el punto P que equidista de A(7,-3), B(8,-2) y C(0,-2).

Ejercicio 6 (7'10") Sinopsis:

La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P.

Ejercicio 7 (6'15") Sinopsis:

Sean los puntos M(5,2) y N(1,k). Determina "k" en cada uno de los siguientes casos:

a) d(M,N)=4; b) d(M,N)=6; c) d(M,N)=1

Polígonos:

Ejercicio 1 (6'21") Sinopsis:

Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1).

Ejercicio 2 (6'21") Sinopsis:

Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1).

Ejercicio 3 (9'17") Sinopsis:

Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón.

Ejercicio 4 (9'17") Sinopsis:

Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón.

Ejercicio 5 (7'56") Sinopsis:

Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área.

Ejercicio 6 (8'04") Sinopsis:

Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área.

Ejercicio 7 (5'46") Sinopsis:

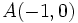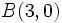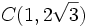Verifica que los puntos $A(-1,0)\;$ , $B(3,0)\;$ y $C(1,2\sqrt{3})$ forman un triángulo equilátero.

Ejercicio 8 (6'04") Sinopsis:

Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles.

Ejercicio 9 (7'54") Sinopsis:

Analizar si el triángulo A(7,3), B(1,-4) y C(3,5) es equilátero.

Puntos colineales:

Ejercicio 1 (6´12") Sinopsis:

Determina si los puntos A(-3,1), B(0,2) y C(6,4) son colineales, usando distancias.

Ejercicio 2 (6´11") Sinopsis:

Determina si los puntos A(321), B(0,0) y C(9,6) son colineales, usando distancias.

Ejercicio 3 (8´12") Sinopsis:

Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias.

Otros:

Ejercicio 1 (7'30") Sinopsis:

Determina los puntos del plano cuya distancia al punto M(3,-5) sea 2.

Distancia entre dos puntos del plano Descripción:

En esta escena podrás ver como se calcula la distancia entre dos puntos del plano.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:C%C3%A1lculo_de_la_distancia_entre_dos_puntos"

-Conocidas las coordenadas de dos puntos del plano, el teorema de Pitágoras nos permite calcular la distancia entre ambos:
+{{distancia entre dos puntos 4ºESO}}
-{{Teorema|titulo=Proposición|enunciado=La '''distancia entre dos puntos''' <math>P(x_1,y_1)\,</math> y <math>Q(x_2,y_2)\,</math> es igual a:
-{{Caja|contenido=<math>d(PQ)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}</math>}}
-|demo=Ver la siguiente escena de Geogebra.
-}}
 {{p}}
+{{Videos: Distancia entre dos puntos del plano}}
 {{Geogebra: distancia entre dos puntos}}
-{{p}}
-{{Video_enlace_julioprofe
-|titulo1=Distancia entre dos puntos
-|duracion=8'37"
-|sinopsis=Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
-|url1=https://www.youtube.com/watch?v=mC7-joiQsK4
-}}
-{{Video_enlace
-|titulo1=Distancia entre dos puntos
-|duracion=6'12"
-|sinopsis=Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
-|url1=https://www.youtube.com/watch?v=ZPR5WeYv3B4&list=PLHwz3md30-3kyfZgB4y53rPmPydQwj6uj&index=3
-}}
 {{p}}

Plantilla:Cálculo de la distancia entre dos puntos

De Wikipedia

Revisión actual

Vistas

Herramientas personales

Menú

Buscar

Herramientas