Resolución de triángulos rectángulos (1ºBach)
De Wikipedia
| Revisión de 13:43 22 feb 2009 Coordinador (Discusión | contribuciones) (→Casos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Resolución de triángulos rectángulos) |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | __TOC__ | ||
| {{p}} | {{p}} | ||
| - | ==Resolución de triángulos== | + | (Pág. 112) |
| - | {{Caja_Amarilla|texto='''Resolver un triángulo''' es hallar los lados y ángulos desconocidos a partir de los conocidos.}} | + | ==Resolución de triángulos rectángulos== |
| + | {{Resolución de triángulos rectángulos}} | ||
| {{p}} | {{p}} | ||
| - | ==Casos== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | *'''Caso 1:''' Nos dan 2 lados. | ||
| - | **El lado que falta se halla por el [[teorema de Pitágoras]]. | ||
| - | **El ángulo que forman los lados conocidos se halla mediante la razón trigonométrica que los relaciona. | ||
| - | *'''Caso 2:''' Nos dan 1 lado y 1 ángulo agudo. | ||
| - | **Uno de los lados se halla mediante la razón trigonométrica que lo relaciona con el lado y el ángulo conocidos. | ||
| - | **El otro ángulo agudo se halla como complementario del que nos dan. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Resolución de triángulos'' | ||
| - | |enunciado= | ||
| - | * '''Caso 1:''' Resuelve un triángulo rectángulo del que nos dan un cateto que mide 11 cm y la hipotenusa que mide 20 cm. | ||
| - | * '''Caso 2:''' Resuelve un triángulo rectángulo del que nos dan un cateto que mide 15 cm y su ángulo contiguo que mide 50º. | ||
| - | |sol=[[Imagen:trianrect.jpg|250px|right]] | + | ==Ejercicios propuestos== |
| - | * '''Caso 1:''' {{sube|porcentaje=15%|contenido=<math>a=11 \, cm; \, c=20 \, cm</math>}} | + | {{ejercicio |
| - | : Por el [[teorema de Pitágoras]] hallamos el cateto {{sube|porcentaje=15%|contenido=<math>b: \quad b=\sqrt{c^2-a^2}=16.7 \, cm</math>}} | + | |titulo=Ejercicios propuestos: ''Resolución de triángulos rectángulos'' |
| - | : El ángulo {{sube|porcentaje=15%|contenido=<math>\hat A: \quad sen \, \hat A= \cfrac{11}{20}=0.55 \rightarrow \hat A=33^\circ 22'</math>}} | + | |cuerpo= |
| - | : Hallamos el ángulo {{sube|porcentaje=15%|contenido=<math>\hat B: \quad \hat B= 90^\circ - \hat A=56^\circ \, 38'</math>}} | + | (Pág. 113) |
| - | * '''Caso 2:''' {{sube|porcentaje=15%|contenido=<math>a=15 \, cm; \, \hat B=50^\circ</math>}} | + | [[Imagen:red_star.png|12px]] 1, 2 |
| - | :Hallamos el cateto {{sube|porcentaje=15%|contenido=<math>b: \quad tg \ \hat B=\cfrac{b}{a} \rightarrow b=a \cdot tg \, \hat B=15 \cdot tag \, 50^\circ=17.88 \, cm</math>}} | + | |
| - | :Hallamos el cateto {{sube|porcentaje=10%|contenido=<math>a: \quad cos \ \hat B=\cfrac{a}{c} \rightarrow c=\cfrac{a}{cos \, \hat B}=\cfrac{15}{cos \, 50^\circ}=23.34 \, cm</math>}} | + | [[Imagen:yellow_star.png|12px]] 3 |
| - | : Hallamos el ángulo {{sube|porcentaje=15%|contenido=<math>\hat A: \quad \hat A= 90^\circ - \hat B=90^\circ - 50^\circ=40^\circ</math>}} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | ==Ejercicios== | ||
| - | {{AI2|titulo=Actividad interactiva: ''Resolución de triángulos''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Triángulos rectángulos | ||
| - | |actividad={{p}} | ||
| - | *Si pulsas el botón "EJERCICIO" cambiarán los datos del problema. | ||
| - | *Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes. | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo10.html | ||
| - | width=710 | ||
| - | height=270 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo10.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' Cálculo de la altura de un árbol o de una cometa. | ||
| - | |actividad={{p}} | ||
| - | *Si pulsas el botón "EJERCICIO" cambiarán los datos del problema. | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo14a.html | ||
| - | width=710 | ||
| - | height=370 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/Trigonometria/trigo14a.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 112)
Resolución de triángulos rectángulos
Resolver un triángulo es hallar los lados y ángulos desconocidos a partir de los conocidos.
Resolución de triángulos rectángulos
- Caso 1: Nos dan 2 lados:
- El lado que falta se halla por el teorema de Pitágoras.
- El ángulo que forman los lados conocidos se halla mediante la razón trigonométrica que los relaciona.
- Caso 2: Nos dan 1 lado y 1 ángulo agudo:
- Uno de los lados se halla mediante la razón trigonométrica que lo relaciona con el lado y el ángulo conocidos.
- El otro ángulo agudo se halla como complementario del que nos dan.
Ejemplos: Resolución de triángulos rectángulos
- Caso 1: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 11 cm y la hipotenusa que mide 20 cm.
- Caso 2: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 15 cm y su ángulo contiguo que mide 50º.
- Caso 1:
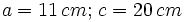
- Hallamos el cateto
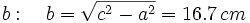 (Por el teorema de Pitágoras)
(Por el teorema de Pitágoras)
- Hallamos el ángulo
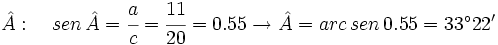
- Hallamos el ángulo
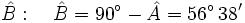
- Caso 2:
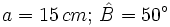
- Hallamos el cateto
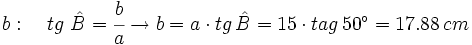
- Hallamos el cateto
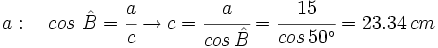
- Hallamos el ángulo
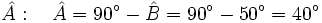
Resolución de triángulos rectángulos. Ejemplos.
Resolución de triángulos rectángulos. Ejemplos.
- Resolver un triángulo es identificarlo; o sea, determinar sus lados y ángulos. Para resolver un triángulo rectángulo basta conocer, además del ángulo recto, un ángulo y un lado o dos de los lados.
- Ejemplos.
En un triángulo rectángulo un ángulo mide 65º y su cateto adyacente mide 5. Usa la calculadora para averiguar los lados que faltan.
En un triángulo rectángulo un ángulo mide 60º y su cateto adyacente mide 20 m. Halla el cateto opuesto sin usar la calculadora.
Resuelve los siguientes triángulos rectángulos:
- Un ángulo mide 25º y su cateto opuesto 8.
- Un cateto mide 12 y la hipotenusa 25.
- Un ángulo mide 70º y la hipotenusa 12.
- Los catetos miden 6 y 16.
Conceptos de ángulo de elevación y de ángulo de depresión.
- Conceptos de ángulo de elevación y de ángulo de depresión.
- Problema:
- Desde la cima de un faro se observa un bote con un ángulo de depresión de 37º. Si el faro tiene una altura de 60 m, calcula la distancia entre el bote y la base del faro.
- A 9.60 m de un poste, una persona de 1.80 m de estatura, divisa lo más alto del poste con un ángulo de elevación de 37º. Halla la altura del poste.
- Resuelve el triángulo rectángulo cuyos catetos miden 6 y 8 cm.
- Resuelve el triángulo rectángulo cuyo cateto mide 8 cm y su ángulo adyacente 60º.
- Determina la sombra proyectada por un árbol de 10 m de altura cuando el sol levanta 30º sobre el horizonte.
Resuelve el triángulo rectángulo cuyos catetos miden 6 y 8 cm, respectivamente.
Resuelve el triángulo rectángulo ABC con ángulo recto en A, si sabemos que el cateto b mide 18.3 cm y el ángulo C vale 50º30'39".
Las diagonales de un rombo miden 10 y 6 cm, respectivamente. Calcula los ángulos del rombo.
Un tren de cremallera se eleva 800 m para ir de un pueblo a otro con una pendiente del 30%. Calcula la distancia entre los dos pueblos.
Calcula la inclinación de la torre de Pisa. Se sabe que su base se separa 3.9 m de la vertical y que llega hasta los 55.7 m de altura.
Para medir la altura de una torre, Isabel, que mide 1.60 m, se sitúa, de pie, a 5 m de la torre, y mide el ángulo que forma la visual al extremo superior de la torre con la horizontal, 70º. Calcula la altura de la torre.
Calcula el radio de un octógono regular de 6 cm de lado.
En una circunferencia de 8 cm de radio, una cuerda mide 6 cm. ¿Cuánto mide el ángulo central que abarca esta cuerda?
Cada brazo de un compás mide 13.5 cm. Si abrimos el compás de manera que la distancia entre la dos puntas sea de 6 cm, ¿qué ángulo formarán los dos brazos?
En el momento en el que la altura del sol es de 50º, la sombra de una torre es de 5 m. ¿Qué altura tiene la torre?
El cable de un telesilla tiene una longitud de 1.5 km y forma un ángulo de 40º con la horizontal. ¿Qué desnivel vertical cubre?
Calcula el ángulo de inclinación de una rampa que sube 0.5 m en 6 m recorridos sobre el plano inclinado.
La altura de un rectángulo es 8 cm y forma un ángulo de 25º con la diagonal. Calcula el área del rectángulo.
¿Cuánto nos elevamos cuando recorremos 750 m por una carretera inclinada 12º?
La apotema de un pentágono regular mide 6 cm. Calcula el lado del pentágono.
A una distancia de 2 m de una pared, apoyamos una escalera que forma 65º con la horizontal. ¿Cuánto mide la escalera?
Desde un faro situado a 70 m de altura, se observa un barco con un ángulo de depresión de 32º. Calcula la distancia del barco a la tierra.
Una calle tiene una anchura de 18 m. ¿Qué altura máxima pueden tener los edificios, de manera que los rayos del sol incidan en el otro lado de la calle formando con el suelo un ángulo de 38º?
Cálculo del área de una pirámide pentagonal
Cálculo de la sombra de una persona a una determinada hora del día.
Un pequeño pero horrible extraterrestre está en la punta de la Torre Eiffel (que mide 324 m de alto), ¡y amenaza destruir toda la ciudad de París! Un agente de los "Hombres de Negro" se encuentra a nivel del suelo, a 54 m de distancia de la Torre Eiffel, apuntando su arma láser al extraterrestre. ¿Con qué ángulo de elevación debe el agente disparar su láser? Da el resultado redondeado a 2 decimales, de ser necesario.
Distintos ejemplos de resolución de problemas de triángulos rectángulos.
Hallar un lado de un triángulo rectángulo a partir de un ángulo y un lado:
Aprende a resolver los lados de un triángulo rectángulo usando razones trigonométricas con calculadora.
Resuelve los lados de un triángulo rectángulo usando razones trigonométricas con calculadora.
Resuelve los lados de un triángulo rectángulo usando razones trigonométricas con calculadora.
Aviso: Antes de hacer la actividad puedes ver algunos ejemplos en: Ejemplos
Hallar un ángulo de un triángulo rectángulo a partir de dos lados:
Aprende a resolver un ángulo de un triángulo rectángulo usando razones trigonométricas recíprocas con calculadora.
Resuelve un ángulo de un triángulo rectángulo usando razones trigonométricas recíprocas con calculadora.
Problemas:
Aprende los conceptos de ángulo de elevación y de depresión.
Repaso de trigonometría de triángulos rectángulos.
En esta escena podrás ver como se calculan alturas de objetos cuya base es accesible.
Problemas resueltos de trigonometría que utilizan el método de observación simple para calcular distancias en triángulos rectángulos.
Problemas de resolución de triángulos rectángulos.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de triángulos rectángulos |