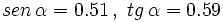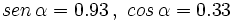Plantilla:Relaciones fundamentales de la trigonometría
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:20 24 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:25 24 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 75: | Línea 75: | ||
| |url1=https://www.youtube.com/watch?v=xePJNWPKSaQ | |url1=https://www.youtube.com/watch?v=xePJNWPKSaQ | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 7 | |titulo1=Ejercicio 7 | ||
| Línea 85: | Línea 84: | ||
| |url1=https://www.youtube.com/watch?v=_GtZv7A386I | |url1=https://www.youtube.com/watch?v=_GtZv7A386I | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 8 | |titulo1=Ejercicio 8 | ||
| Línea 91: | Línea 89: | ||
| |sinopsis=Comprueba la siguiente identidad trigonométrica: | |sinopsis=Comprueba la siguiente identidad trigonométrica: | ||
| - | :<math>cos^4 x - sen^4 x +1 = 2 cos^2 x</math> | + | :<math>cos^4 x - sen^4 x +1 = 2 cos^2 x\;</math> |
| |url1=https://www.youtube.com/watch?v=oko2J_mU0VI | |url1=https://www.youtube.com/watch?v=oko2J_mU0VI | ||
| }} | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=8'39" | ||
| + | |sinopsis=Comprueba la siguiente identidad trigonométrica: | ||
| + | :<math>\cfrac{sen^4 \alpha - cos^4 \alpha + 1}{1 + cotg^2 \alpha}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=cmco_-I1KEI | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:25 24 may 2017
Relaciones fundamentales de la trigonometría
1. 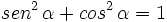
2. 
3. 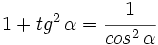
Demostración:
Demostración de las relaciones fundamentales de la trigonometría.
En este vídeo nos dan una de las seis razones trigonométricas de un ángulo y debemos determinar las cinco restantes, haciendo uso de las relaciones fundamentales de la trigonometría.
Simplifica: 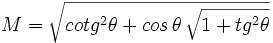
Comprueba las siguientes identidades trigonométricas:
a) 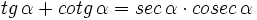
b) 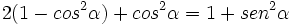
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:
Comprueba la siguiente identidad trigonométrica:

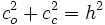
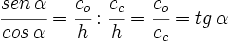
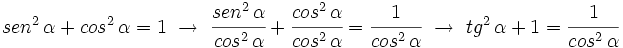
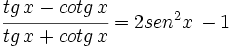
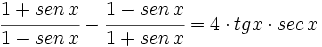
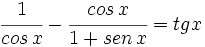
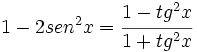
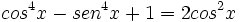
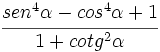
 un ángulo agudo.
un ángulo agudo.

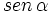 y
y 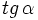 .
.
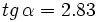
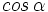 .
.