Plantilla:Ecuación de segundo grado: definición y resolución

De Wikipedia

(Diferencia entre revisiones)

Revisión de 18:47 1 jun 2017

Ecuación de segundo grado

Una ecuación de segundo grado con una incógnita, $x\;\!$ , es aquella que tiene la siguiente expresión, que llamaremos forma general.

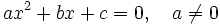
$ax^2+bx+c=0, \quad a\ne 0$

Resolución de la ecuación de segundo grado

Fórmula general

Las soluciones de la ecuación de segundo grado

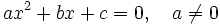
$ax^2+bx+c=0, \quad a\ne 0$

son:

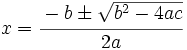
$x=\cfrac{-b \pm \sqrt {b^2-4ac}}{2a}$

donde el signo 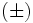$(\pm)$ significa que una solución se obtiene con el signo 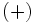$(+)\;\!$ y otra con el signo $(-)\;\!$ .

Demostración:

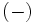1. Se divide la ecuación por $a\;\!$ :

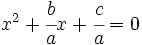
$x^2+ \cfrac{b}{a}x+ \cfrac{c}{a}=0$

2. Se multiplica y divide por $2\;\!$ el coeficiente de la $x\;\!$ :

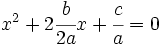
$x^2+ 2\cfrac{b}{2a}x+ \cfrac{c}{a}=0$

3. Se suma a los dos miembros de la igualdad 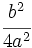$\cfrac{b^2}{4a^2}$ :

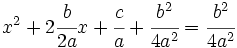
$x^2+ 2\cfrac{b}{2a}x+ \cfrac{c}{a}+ \cfrac{b^2}{4a^2}=\cfrac{b^2}{4a^2}$

4. Se pasa restando a la derecha $\cfrac{c}{a}$ :

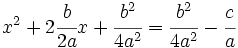
$x^2+ 2\cfrac{b}{2a}x+ \cfrac{b^2}{4a^2}=\cfrac{b^2}{4a^2}- \cfrac{c}{a}$

5. Observando que el lado izquierdo es el desarrollo de 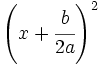$\left ( x+\cfrac{b}{2a} \right )^2$ :

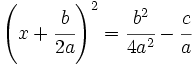
$\left ( x+\cfrac{b}{2a} \right )^2=\cfrac{b^2}{4a^2}- \cfrac{c}{a}$

6. Se extrae la raíz cuadrada en ambos miembros:

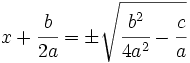
$x+\cfrac{b}{2a}=\pm \sqrt{\cfrac{b^2}{4a^2}- \cfrac{c}{a}}$

7. Se despeja x:

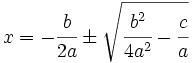
$x=- \cfrac{b}{2a} \pm \sqrt{\cfrac{b^2}{4a^2}- \cfrac{c}{a}}$

8. Se simplifica la expresión:

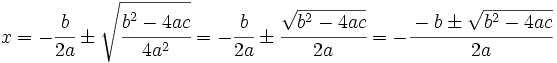
$x=- \cfrac{b}{2a} \pm \sqrt{\cfrac{b^2-4ac}{4a^2}}=- \cfrac{b}{2a} \pm \cfrac{\sqrt{b^2-4ac}}{2a}=- \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

Ejemplos: Ecuaciones de segundo grado resueltas

En la escena, pulsa "Inicio" para ver otros ejemplos.

Ecuación de segundo grado completa

Tutorial 1 (7'37") Sinopsis:

Resolución de ecuaciones de segundo grado completas. Ejemplos.

Tutorial 2 (7'37") Sinopsis:

Cómo utilizar la fórmula general de la ecuación de segundo grado.

Ejercicio 1 (6'05") Sinopsis:

Resuelve: 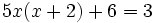$5x(x+2)+6=3\;$

Resolución de la ecuación de segundo grado (2 métodos) (11'36") Sinopsis:

A veces es posible resolver la ecuación de segundo grado por el llamado método de factorización. Cuando no se pueda por este método recurriremos a la fórmula general. En este video puedes ver un ejemplo de cada método.

Resuelve las siguientes ecuaciones de segundo grado Descripción:

Pulsa el botón "Ejercicio" para obtener una ecuación.
Copia la ecuación en tu cuaderno y halla sus soluciones.
Escribe el "tipo de solución" y las soluciones en los cuadros correspondientes. Luego pulsa el botón "Solución".

Resolución de las ecuaciones de segundo grado

Actividad: Resolución de las ecuaciones de segundo grado

Resuelve las siguientes ecuaciones:

a) $4x^2+4x+1=0 \;$

b) $4x^2-25=0 \;$

c) $x^2+x-12=0 \;$

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) solve 4x^2+4x+1=0 b) solve 4x^2-25=0 c) solve x^2+x-12=0

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Ecuaci%C3%B3n_de_segundo_grado:_definici%C3%B3n_y_resoluci%C3%B3n"

 <center><math>x=- \cfrac{b}{2a} \pm \sqrt{\cfrac{b^2-4ac}{4a^2}}=- \cfrac{b}{2a} \pm \cfrac{\sqrt{b^2-4ac}}{2a}=- \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}</math></center>
-}}
-{{p}}
-{{Video_enlace_carreon
-|titulo1=Ejemplos
-|duracion=7'37"
-|sinopsis=Cómo utilizar la fórmula general de la ecuación de segundo grado.
-|url1=https://www.youtube.com/watch?v=Wj4cHg8oHzI
 }}
 {{p}}
 }}
 {{p}}
+{{Videotutoriales|titulo=Ecuación de segundo grado completa|enunciado=
+{{Video_enlace_tutomate
+|titulo1=Tutorial 1
+|duracion=7'37"
+|sinopsis=Resolución de ecuaciones de segundo grado completas. Ejemplos.
+|url1=https://www.youtube.com/watch?v=Wj4cHg8oHzI
+}}
+{{Video_enlace_carreon
+|titulo1=Tutorial 2
+|duracion=7'37"
+|sinopsis=Cómo utilizar la fórmula general de la ecuación de segundo grado.
+|url1=https://www.youtube.com/watch?v=Wj4cHg8oHzI
+}}
 {{Video_enlace_julioprofe
-|titulo1=Ejemplo
+|titulo1=Ejercicio 1
 |duracion=6'05"
 |sinopsis=Resuelve: <math>5x(x+2)+6=3\;</math>
 |url1=https://www.youtube.com/watch?v=xmzG2xR-oBI
 }}
-{{p}}
+{{Video_enlace_abel
-{{Video_enlace
 |titulo1=Resolución de la ecuación de segundo grado (2 métodos)
 |duracion=11'36"
 |sinopsis=A veces es posible resolver la ecuación de segundo grado por el llamado [https://www.youtube.com/watch?v=RChv5xhNTgY método de factorización]. Cuando no se pueda por este método recurriremos a la fórmula general. En este video puedes ver un ejemplo de cada método.
 |url1=https://www.youtube.com/watch?v=2fYqL5gqXOs
+}}
 }}
 {{p}}

Plantilla:Ecuación de segundo grado: definición y resolución

De Wikipedia

Revisión de 18:47 1 jun 2017

Ecuación de segundo grado

Resolución de la ecuación de segundo grado

Vistas

Herramientas personales

Menú

Buscar

Herramientas