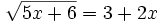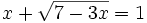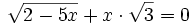Plantilla:Ecuaciones con radicales
De Wikipedia
| Revisión de 18:55 14 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Resolución de las ecuaciones radicales) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Las '''ecuaciones con radicales''' son aquellas que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas. | + | {{Caja_Amarilla|texto=Las '''ecuaciones con radicales''' o '''ecuaciones irracionales''' son aquellas que tienen la incógnita bajo el signo radical. |
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo | ||
| + | |titulo=Resolución de las ecuaciones radicales | ||
| + | |enunciado= | ||
| + | Para resolver las ecuaciones con radicales hay que aislar las raices, una a una, e ir elevando al cuadrado ambos miembros de la ecuación para eliminarlas. | ||
| Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que '''hacer la comprobación''' en la ecuación inicial para detectar y recharzar las que no sean válidas. | Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que '''hacer la comprobación''' en la ecuación inicial para detectar y recharzar las que no sean válidas. | ||
| Línea 5: | Línea 11: | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Ecuaciones con radicales | + | {{Ejemplo|titulo=Ejercicios resueltos: ''Ecuaciones con radicales |
| |enunciado=Resuelve las ecuaciones: | |enunciado=Resuelve las ecuaciones: | ||
| - | ::a) <math>\sqrt{3x-5} +1=x\;\! </math> | ||
| - | ::b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4 \;\! </math> | + | :a) <math>\sqrt{2x-3} +1=x\;\! </math> |
| + | |||
| + | :b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4 \;\! </math> | ||
| |sol= | |sol= | ||
| - | a) <math>\sqrt{3x-5} +1=x</math> | + | a) <math>\sqrt{2x-3} +1=x</math> |
| - | <math>\sqrt{3x-5}=x-1</math> | + | Aislamos la raíz: |
| + | |||
| + | <math>\sqrt{2x-3}=x-1</math> | ||
| Se elevan al cuadrado los dos lados de la ecuación: | Se elevan al cuadrado los dos lados de la ecuación: | ||
| - | <math>3x-5=x^2-2x+1 \rightarrow x^2 -5x + 6 \rightarrow x_1=2 \ x_2=3 \,\!</math> | + | <math>2x-3=x^2-2x+1 \rightarrow x^2 -4x + 4 \rightarrow x=2 \ (doble)</math> |
| - | Comprobación: <math>\begin{cases} \sqrt{3 \cdot 2 - 5} + 1 = \sqrt{1} + 1 = 2 \ \mbox{valida} \\ \sqrt{3 \cdot 3 - 5} + 1 = \sqrt{4} + 1 = 3 \ \mbox{valida} \end{cases}</math> | + | '''Comprobación:''' <math>\sqrt{2 \cdot 2 - 3} + 1 = \sqrt{1} + 1 = 2 </math> |
| + | |||
| + | Luego es válida <math>x=2 \;</math>. | ||
| ---- | ---- | ||
| Línea 26: | Línea 37: | ||
| b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4</math> | b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4</math> | ||
| - | Despejamos la primera raíz (Podíamos haber empezado por la segunda) | + | Aislamos una de las dos raíces: |
| <math>\sqrt{2x-3} = 4 - \sqrt{x+7}</math> | <math>\sqrt{2x-3} = 4 - \sqrt{x+7}</math> | ||
| - | Se elevan al cuadrado los dos lados del igual | + | Se elevan al cuadrado los dos lados de la ecuación: |
| <math>2x-3 = 16 + (x+7) -8\sqrt{x+7}</math> | <math>2x-3 = 16 + (x+7) -8\sqrt{x+7}</math> | ||
| - | Aislamos la raíz | + | Aislamos la raíz: |
| <math>x -26 = -8\sqrt{x+7}</math> | <math>x -26 = -8\sqrt{x+7}</math> | ||
| - | Se elevan al cuadrado los dos lados del igual | + | Se elevan al cuadrado los dos lados de la ecuación: |
| - | <math>x^2-52x+676=64(x+7) \rightarrow x^2-116x+228=0 \rightarrow x_1=2 \ x_2=114</math> | + | <math>x^2-52x+676=64(x+7) \rightarrow x^2-116x+228=0 \rightarrow \begin{cases}x_1=2 \\ x_2=114 \end{cases}</math> |
| - | Comprobación <math>\begin{cases} x_1=2 \rightarrow \sqrt{2 \cdot 2 -3} \sqrt{2+7}=\sqrt{1}+\sqrt{9} = 1+3=4 \ \mbox{valida} \\ x_2=114 \rightarrow \sqrt{2 \cdot 114 - 3} + \sqrt{114+7}=15+11 \ne 4 \ \mbox{no valida} \end{cases}</math> | + | '''Comprobación:''' <math>\begin{cases} x_1=2 \rightarrow \sqrt{2 \cdot 2 -3} + \sqrt{2+7}=\sqrt{1}+\sqrt{9} = 1+3=4 \\ x_2=114 \rightarrow \sqrt{2 \cdot 114 - 3} + \sqrt{114+7}=15+11 \ne 4 \end{cases}</math> |
| + | |||
| + | Sólo es válida <math>x_1=2 \;</math> | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{videos ecuaciones con radicales}} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Ecuaciones con radicales|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Ecuaciones con radicales'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | Resuelve las siguientes ecuaciones: | ||
| + | |||
| + | :a) <math>\sqrt{5x+6}=3+2x </math> | ||
| + | |||
| + | :b) <math>x+\sqrt{7-3x}=1 </math> | ||
| + | |||
| + | :c) <math>\sqrt{2-5x}+x\cdot \sqrt{3}=0 </math> | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=solve sqrt(5x+6)=3+2x}} {{b4}} b) {{consulta|texto=solve x+sqrt(7-3x)=1}} {{b4}} c) {{consulta|texto=solve sqrt(2-5x)+x*sqrt(3)=0}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
Revisión actual
Las ecuaciones con radicales o ecuaciones irracionales son aquellas que tienen la incógnita bajo el signo radical.
Resolución de las ecuaciones radicales
Para resolver las ecuaciones con radicales hay que aislar las raices, una a una, e ir elevando al cuadrado ambos miembros de la ecuación para eliminarlas.
Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que hacer la comprobación en la ecuación inicial para detectar y recharzar las que no sean válidas.
Ejercicios resueltos: Ecuaciones con radicales
Resuelve las ecuaciones:
- a)
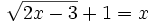
- b)
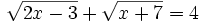
a) 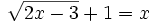
Aislamos la raíz:
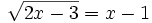
Se elevan al cuadrado los dos lados de la ecuación:
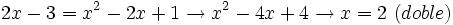
Comprobación: 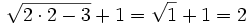
Luego es válida  .
.
b) 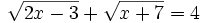
Aislamos una de las dos raíces:
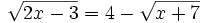
Se elevan al cuadrado los dos lados de la ecuación:
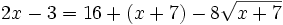
Aislamos la raíz:
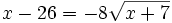
Se elevan al cuadrado los dos lados de la ecuación:
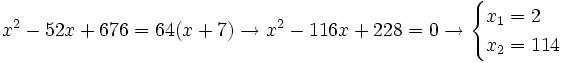
Comprobación: 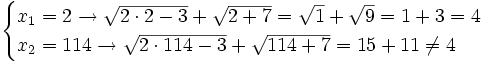
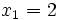
Ecuaciones con radicales. Ejemplos.
Tutorial que explica de forma completa la resolución de ecuaciones con radicales, resolviendo muchos ejercicios desde muy sencillos, para entender mejor la estrategia a seguir, hasta más completos.
- 1) (00:57)
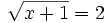
- 2) (03:10)
![\sqrt[3]{x-2}+2 =0\;](/wikipedia/images/math/d/4/a/d4add67bb84f722d8cb6a162e6f59344.png)
- 3) (04:40)
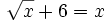
- 4) (11:28)
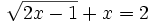
- 5) (14:12)
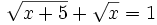
- 6) (19:20)
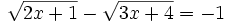
Ecuaciones irracionales, que son aquellas con radicales.
Ecuaciones irracionales, que son aquellas con radicales.
Resuelve: a) b) Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: | Resuelve: Resuelve: Resuelve: Resuelve: 3 ecuaciones con radicales. |
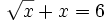
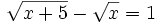
![7+\sqrt[3]{5x-2}=9\;](/wikipedia/images/math/6/a/f/6af645df30220f04516e2fc14bef6f9a.png)
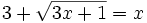
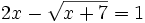
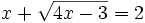
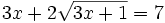
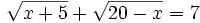
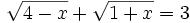
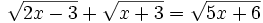
![\sqrt[3]{x+3}=\sqrt{x-1}\;](/wikipedia/images/math/b/0/4/b04567c4f2bc400f01cf3b70e3100545.png)