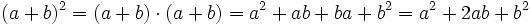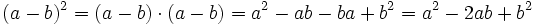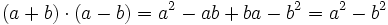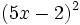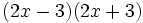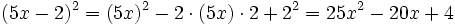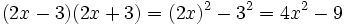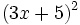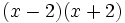Plantilla:Identidades notables
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:05 3 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:06 3 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 49: | Línea 49: | ||
| {{Videotutoriales|titulo=Identidades notables|enunciado= | {{Videotutoriales|titulo=Identidades notables|enunciado= | ||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| - | |titulo1=Tutorial 1 | + | |titulo1=Identidades notables |
| |duracion=9'38" | |duracion=9'38" | ||
| |sinopsis=Productos notables. Ejemplos. | |sinopsis=Productos notables. Ejemplos. | ||
| Línea 56: | Línea 56: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=Identidades notables (ampliado) |
| |duracion=25'26" | |duracion=25'26" | ||
| |sinopsis=Explicación de las igualdades o identidades notables y ejemplos resueltos. | |sinopsis=Explicación de las igualdades o identidades notables y ejemplos resueltos. | ||
Revisión de 07:06 3 jun 2017
Productos notables
- Cuadrado de una suma:
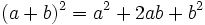
- Cuadrado de una diferencia:

- Suma por diferencia:
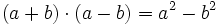
Demostración:
- Cuadrado de una suma:
Escena que demuestra geométricamente la fórmula del cuadrado de una suma
- Cuadrado de una diferencia:
Escena que demuestra geométricamente la fórmula del cuadrado de una diferencia
- Suma por diferencia:
Escena que demuestra geométricamente la fórmula de la suma por diferencia
Productos notables. Ejemplos.
Explicación de las igualdades o identidades notables y ejemplos resueltos.
- Fórmulas del cuadrado de una suma y de una diferencia.
- Ejemplos::
- a)

- b)
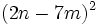
- Fórmula de la suma por diferencia.
- Ejemplos:
- a)
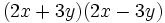
- b)
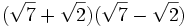
- c)
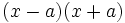
Desarrolla:
- a)
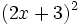
- b)
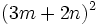
- c)
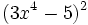
- d)
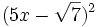
Desarrolla:
- a)
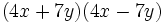
- b)
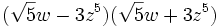
- c)

Desarrolla: 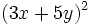
Desarrolla: 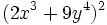
Desarrolla: 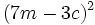
Desarrolla: 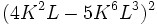
Desarrolla: 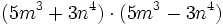
Desarrolla:
a) 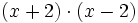
b) 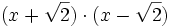
c) 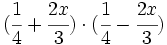
d) 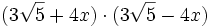
e) 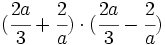
- Cubo de una suma:
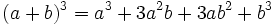
- Cubo de una diferencia:
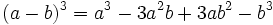
- Ejemplos.
- Suma de cubos:
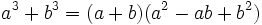
- Diferencia de cubos:
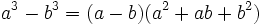
- Ejemplos.
- Cuadrado de un trinomio:
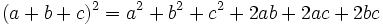
- Ejemplos.