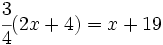Plantilla:Resolución de ecuaciones de primer grado

De Wikipedia

(Diferencia entre revisiones)
Revisión de 09:48 6 jun 2017
Coordinador (Discusión | contribuciones)
(→Actividades y videotutoriales)
← Ir a diferencia anterior		 Revisión de 09:50 6 jun 2017
Coordinador (Discusión | contribuciones)
(→Casos especiales)
Ir a siguiente diferencia →
Línea 102: Línea 102:
}} }}
{{p}} {{p}}
-{{Videotutoriales|titulo=Ecuaciones de primer grado|enunciado=+{{Videotutoriales|titulo=Resolución de ecuaciones de primer grado|enunciado=
-{{Video_enlace_clasematicas+
-|titulo1=Tutorial+
-|duracion=41´52"+
-|url1=https://www.youtube.com/watch?v=74jf7ma8YYs&index=2&list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eg+
-|sinopsis=Todo lo que necesitas saber para resolver ecuaciones de primer grado. Tutorial que explica de forma completa la resolución de ecuaciones de primer grado, empezando con algunos conceptos teóricos y resolviendo muchos ejericios desde muy sencillos, para entender mejor las propiedades de la regla de la suma y del producto, hasta más completos.+
- +
-*0:00 Introducción+
-*0:40 Definiciones: ecuaciones, expresión algebraica.+
-*2:34 Definiciones: Identidad y absurdo.+
-*4:29 Definiciones: Soluciones de una ecuación.+
-*5:36 Cómo comprobar una solución / cómo se resuelve.+
-*8:20 Propiedades: grados de una ecuación y número de soluciones.+
-*9:49 Propiedades: Regla de la suma.+
-*13:40 Propiedades: Regla del producto.+
-*15:58 Despejar la variable (resolver una ecuación).+
-*22:40 Pasos a seguir para resolver cualquier ecuación de primer grado.+
-*25:13 Ejemplos: Ejemplo 1 (con paréntesis).+
-*28:10 Ejemplos: Ejemplo 2 (con denominadores).+
-*31:21 Ejemplos: Ejemplo 3 (con denominador sólo en un lado).+
-*34:14 Ejemplos: Ejemplo 4 (fracciones y paréntesis).+
-*38:15 Identificando identidad y absurdo.+
-}}+
-----+
{{Video_enlace_julioprofe {{Video_enlace_julioprofe
|titulo1=Ejercicio 1 |titulo1=Ejercicio 1

Revisión de 09:50 6 jun 2017

ejercicio

Procedimiento

Para resolver una ecuación de primer grado hay que transformarla en otras ecuaciones equivalentes, cada vez más sencillas, hasta conseguir despejar la incógnita.

Los pasos que hay que dar pueden ser los siguientes, aunque algunos pueden variar de orden según los casos:

  1. Quitar denominadores, si los hay (multiplicando los dos miembros de la ecuación por el mínimo común múltiplo de los denominadores).
  2. Quitar paréntesis, si los hay.
  3. Transponer términos, pasando las incógnitas a un lado y los números al otro (Usaremos la primera de las transformaciones descritas en el apartado anterior)
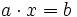  4. Simplificar cada miembro (agrupando términos numéricos y términos con incógnita) hasta obtener una expresión del tipo a \cdot x = b.
  5. Despejar la incógnita, x, obteniendo la solución (Usaremos la segunda de las transformaciones descritas en el apartado anterior, siempre que 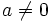a \ne 0. Si fuese 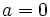a=0\,, estaremos un caso especial que se analizará en el apartado de "casos especiales".)
  6. Podemos, opcionalmente, comprobar la solución. Para ello sustituiremos la incógnita por la solución en los dos miembros de la ecuación de partida y los resultados deben coincidir.

ejercicio

Ejercicios resueltos

Resuelve la siguiente ecuación:

\cfrac{3x-1}{20}-\cfrac{2(x+3)}{5}=\cfrac{4x+2}{15}-5
Solución:
Solución: x=7\,

ejercicio
Ejemplos: Ecuaciones de primer grado sencillas

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

ejercicio
Ejemplos: Ecuaciones de primer grado con paréntesis

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

ejercicio
Ejemplos: Ecuaciones de primer grado con denominadores

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

Casos especiales

Tras efectuar el procedimiento anterior, si en la expresión 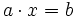a \cdot x=b\; del paso 4º resulta que 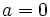a=0\,, al no poder dividir por 0 para despejar la x (paso 5º), llegaremos a uno de los siguientes dos casos especiales:

ejercicio

Casos especiales

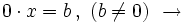  • 0 \cdot x = b \, , \ (b \ne 0) \ \rightarrow La ecuación no tiene solución.
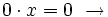  • 0 \cdot x = 0 \ \rightarrow La ecuación tiene infinitas soluciones.
Demostración:
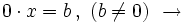  • 0 \cdot x = b \, , \ (b \ne 0) \ \rightarrow Si b es distinto de cero, como el miembro de la izquierda es siempre cero, la igualdad es imposible. Por tanto no hay solución.
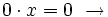  • 0 \cdot x = 0 \ \rightarrow El miembro de la izquierda es siempre cero, por tanto, sea cual sea el valor de x, la igualdad se cumple. Luego, cualquier número es solución de la ecuación.

ejercicio
Ejemplos
  • 3x-7=3x \ \rightarrow \ 0 \cdot x = 7 \ \rightarrow No tiene solución, ya que no hay ningún número que multiplicado por 0 de 7.
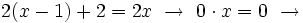  • 2(x-1)+2 = 2x \ \rightarrow \ 0 \cdot x = 0 \ \rightarrow La ecuación tiene infinitas soluciones, ya que cualquier número multiplicado por 0 da 0.

wolfram
Resolución de ecuaciones de primer grado
wolfram

Actividad: Resolución de ecuaciones de primer grado

Resuelve las siguientes ecuaciones:

a) \cfrac{x-1}{4}-\cfrac{x-5}{36}=\cfrac{x+5}{9}\;
b) \cfrac{3}{4}(2x+4)=x+19 \;

Solución:
Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
a) solve (x-1)/4 - (x-5)/36 = (x+5)/9
b) solve 3/4 (2x+4)=x+19

video
Resolución de ecuaciones de primer grado
Ejercicio 1 (6'16")     Sinopsis:

Resuelve: 15x-[8x-(2-10x)]=24x+[-(3x+7)-(x+1)]\;

Ejercicio 2 (5'29")     Sinopsis:

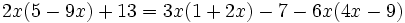
Resuelve: 2x(5-9x)+13=3x(1+2x)-7-6x(4x-9)\;

Ejercicio 3 (7'42")     Sinopsis:

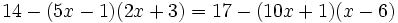
Resuelve: 14-(5x-1)(2x+3)=17-(10x+1)(x-6)\;

Ejercicio 4 (7'26")     Sinopsis:

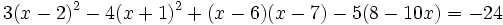
Resuelve: 3(x-2)^2-4(x+1)^2+(x-6)(x-7)-5(8-10x)=-24\;

Ejercicio 5 (3'12")     Sinopsis:

Resuelve: \cfrac{4}{x-3}=\cfrac{5}{x-2}\;

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Resoluci%C3%B3n_de_ecuaciones_de_primer_grado"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda