Plantilla:Videos: Distancia entre dos puntos del plano
De Wikipedia
| Revisión de 11:00 18 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:06 18 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| }} | }} | ||
| ---- | ---- | ||
| - | Triángulos: | + | Polígonos: |
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| |titulo1=Ejercicio 7 | |titulo1=Ejercicio 7 | ||
| + | |duracion=6'21" | ||
| + | |sinopsis=Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1). | ||
| + | |url1=https://www.youtube.com/watch?v=kFxV2O8Ib7E&index=1&list=PLo7_lpX1yruPqdVhqpI0YmCbyZ1jIBerc | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=6'21" | ||
| + | |sinopsis=Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1). | ||
| + | |url1=https://www.youtube.com/watch?v=QFdZWJ7NjmA&list=PLo7_lpX1yruPqdVhqpI0YmCbyZ1jIBerc&index=2 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 9 | ||
| |duracion=9'17" | |duracion=9'17" | ||
| |sinopsis=Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón. | |sinopsis=Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón. | ||
| Línea 67: | Línea 79: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 8 | + | |titulo1=Ejercicio 10 |
| |duracion=9'17" | |duracion=9'17" | ||
| |sinopsis=Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón. | |sinopsis=Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón. | ||
| Línea 73: | Línea 85: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 9 | + | |titulo1=Ejercicio 11 |
| |duracion=7'56" | |duracion=7'56" | ||
| |sinopsis=Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área. | |sinopsis=Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área. | ||
| Línea 79: | Línea 91: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 10 | + | |titulo1=Ejercicio 12 |
| |duracion=8'04" | |duracion=8'04" | ||
| |sinopsis=Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área. | |sinopsis=Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área. | ||
| Línea 85: | Línea 97: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 11 | + | |titulo1=Ejercicio 13 |
| |duracion=5'46" | |duracion=5'46" | ||
| |sinopsis=Verifica que los puntos <math>A(-1,0)\;</math>, <math>B(3,0)\;</math> y <math>C(1,2\sqrt{3})</math> forman un triángulo equilátero. | |sinopsis=Verifica que los puntos <math>A(-1,0)\;</math>, <math>B(3,0)\;</math> y <math>C(1,2\sqrt{3})</math> forman un triángulo equilátero. | ||
| Línea 91: | Línea 103: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 12 | + | |titulo1=Ejercicio 14 |
| |duracion=6'04" | |duracion=6'04" | ||
| |sinopsis=Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles. | |sinopsis=Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles. | ||
| Línea 100: | Línea 112: | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 13 | + | |titulo1=Ejercicio 15 |
| |duracion=6´12" | |duracion=6´12" | ||
| |url1=https://www.youtube.com/watch?v=XWf2aTgZnKo&index=1&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm | |url1=https://www.youtube.com/watch?v=XWf2aTgZnKo&index=1&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm | ||
| Línea 106: | Línea 118: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 14 | + | |titulo1=Ejercicio 16 |
| |duracion=6´11" | |duracion=6´11" | ||
| |url1=https://www.youtube.com/watch?v=BHSCLoW-kA0&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=2 | |url1=https://www.youtube.com/watch?v=BHSCLoW-kA0&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=2 | ||
| Línea 112: | Línea 124: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 15 | + | |titulo1=Ejercicio 17 |
| |duracion=8´12" | |duracion=8´12" | ||
| |url1=https://www.youtube.com/watch?v=og2G0zmxnSk&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=3 | |url1=https://www.youtube.com/watch?v=og2G0zmxnSk&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=3 | ||
Revisión de 11:06 18 jun 2017
Tutorial 1 (8´59") Sinopsis:- Módulo de un vector = distancia entre dos puntos. Demostración de la fórmula.
- Ejemplos y ejercicios.
Tutorial 2 (8'37") Sinopsis: Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Tutorial 3 (6'12") Sinopsis:Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Ejercicio 1 (5'11") Sinopsis: Halla el valor de "x" para que la distancia entre los puntos A(x,-1) y B(9,4) sea 13.
Ejercicio 2 (4'30") Sinopsis: Halla el valor de "y" para que la distancia entre los puntos P(7,1) y Q(3,y) sea 5.
Ejercicio 3 (6'09") Sinopsis: Halla el punto Q el eje Y que equidista de A(4,2) y B(5,5).
Ejercicio 4 (5'26") Sinopsis: Halla el punto P el eje X que equidista de A(5,1) y B(0,6).
Ejercicio 5 (11'53") Sinopsis: Halla el punto P que equidista de A(7,-3), B(8,-2) y C(0,-2).
Ejercicio 6 (7'10") Sinopsis: La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P.
Polígonos:
Ejercicio 7 (6'21") Sinopsis: Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1).
Ejercicio 8 (6'21") Sinopsis: Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1).
Ejercicio 9 (9'17") Sinopsis: Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón.
Ejercicio 10 (9'17") Sinopsis: Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón.
Ejercicio 11 (7'56") Sinopsis: Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área.
Ejercicio 12 (8'04") Sinopsis: Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área.
Ejercicio 13 (5'46") Sinopsis: Verifica que los puntos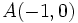 
, 
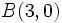y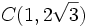 
forman un triángulo equilátero.
Ejercicio 14 (6'04") Sinopsis: Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles.
Puntos colineales:
Ejercicio 15 (6´12") Sinopsis: Determina si los puntos A(-3,1), B(0,2) y C(6,4) son colineales, usando distancias.
Ejercicio 16 (6´11") Sinopsis: Determina si los puntos A(321), B(0,0) y C(9,6) son colineales, usando distancias.
Ejercicio 17 (8´12") Sinopsis: Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias.
