Plantilla:Entre dos racionales hay infinitos racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:41 18 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:42 18 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| '''Demostración:''' | '''Demostración:''' | ||
| - | Por la proposición anterior, si <math>x_1\;</math> y <math>x_2\;</math>; son números racionales, entonces <math>x_m\;</math> también lo es.}} | + | Bastará aplicar la proposición anterior de forma reiterada, y tener en cuenta que si <math>x_1\;</math> y <math>x_2\;</math> son números racionales, entonces <math>x_m\;</math> también lo es. }} |
Revisión de 16:42 18 jun 2017
Proposición
Dados dos puntos, 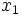 y
y 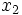 , de la recta numérica, el punto medio,
, de la recta numérica, el punto medio, 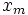 entre esos dos puntos viene dado por
entre esos dos puntos viene dado por
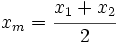
Halla el punto medio entre 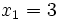 y
y 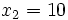 .
.
Halla el punto medio entre 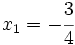 y
y 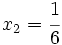 .
.
Halla el punto medio entre 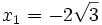 y
y 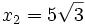 .
.

