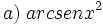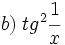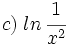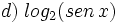Plantilla:Reglas de derivación (1ºBach)
De Wikipedia
| Revisión de 17:35 20 jun 2017 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 17:46 20 jun 2017 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 612: | Línea 612: | ||
| <math>y=\cfrac{x\sqrtt{x+1}}{x+1}\;</math> | <math>y=\cfrac{x\sqrtt{x+1}}{x+1}\;</math> | ||
| |url1=https://www.youtube.com/watch?v=HVG0pOcpP98&index=4&list=PLo7_lpX1yruP3HJwLO-1zoGo_-m6p8QQR | |url1=https://www.youtube.com/watch?v=HVG0pOcpP98&index=4&list=PLo7_lpX1yruP3HJwLO-1zoGo_-m6p8QQR | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | {{Videotutoriales | ||
| + | |titulo=Ejercicios: ''Derivadas de funciones trigonométricas'' | ||
| + | |enunciado= | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=3'04" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=-10x+3\,cos \, x\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=dLWNtdGorlU&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep&index=1 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=3'59" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=\cfrac{3}{x}+ 5\,sen\,x\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=hu87UiiN470&index=2&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=3'21" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=x^2\,cos \, x\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=xLOfKrPYGdE&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep&index=3 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=3'57" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=2x\,sec \, x + 3\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=3qff1Wp_zzI&index=4&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=4'46" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=tg \, x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=ldsGqfFiarc&index=5&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=5'41" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=cotg \, x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=9yk0uGU8DXI&index=6&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=4'30" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=sec \, x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=2HBboVrE6m8&index=7&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=4'40" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=cosec \, x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=OrvVODajGeE&index=8&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=4'10" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=2\,sen\,x \, cos\,x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=2AvpeMPmUKY&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep&index=9 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=4'14" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=2x\,cos\,x -2\,sen\,x;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=oYSy6DjPX8Q&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep&index=10 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=7'30" | ||
| + | |sinopsis=Calcula la derivada de: | ||
| + | <math>y=\cfrac{(x-1)^2}{x\,sen\,x)};</math> | ||
| + | |url1=https://www.youtube.com/watch?v=WvzZqq5JSKE&list=PLo7_lpX1yruN5SO6BEx3qe_LbKDCnUyep&index=11 | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 17:46 20 jun 2017
Hemos visto en el apartado anterior como se obtiene la función derivada de una función. Es un proceso largo y pesado. Existen una serie de reglas, demostradas por medio de ese procedimiento, que nos permitirán aliviar el trabajo del cálculo de la función derivada.
Derivada de las funciones elementales
Reglas de derivación
- Función constante:
- Función identidad:
- Función potencia:
- Funciones trigonométricas directas:
- Funciones trigonométricas recíprocas:
- Funciones exponenciales:
- Funciones logarítmicas:
Derivada de operaciones con funciones
Reglas de derivación
Definición de la función derivada de una función. Las reglas de derivación nos permiten calcular derivadas sin calcular límites.
Demostración de la fórmula de la derivada de un producto.
- 22 ejemplos sencillos de aplicación de las reglas de derivación.
Ejemplos de cálculo de la derivada de una función usando las reglas de derivación.
Halla la derivada de: 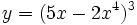
Halla la derivada de: ![y=\sqrt[5]{\cfrac{x^3-2}{x^3+2}}\;](/wikipedia/images/math/9/3/f/93fd87688688e4d63dcfe9b7bc99b928.png)
Halla la derivada de: 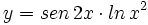
Halla la derivada de:
a) 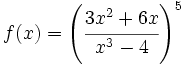
b) 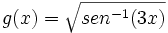
c) 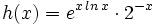
d) ![i(x)=log_2 \, \sqrt[3]{\cfrac{3-x}{x+3}}\;](/wikipedia/images/math/5/4/2/542b0c4ce849272714ecda159e2dc61f.png)
Reglas de derivación de las funciones trigonométricas para casos simple y para casos complejos aplicando la regla de la cadena. Ejemplos.
Reglas de derivación de las funciones exponenciales para casos simple y para casos complejos aplicando la regla de la cadena. Ejemplos.
Reglas de derivación de las funciones logarítmicas para casos simple y para casos complejos aplicando la regla de la cadena. Ejemplos.
Reglas de derivación de las funciones trigonométricas inversas para casos simple y para casos complejos aplicando la regla de la cadena. Ejemplos.
Videotutorial
Ejercicios
Calcula la derivada de:
- 1.
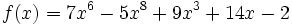
- 2.
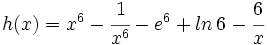
Calcula la derivada de:
- 3.
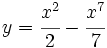
- 4.
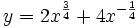
- 5.
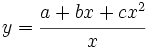
Calcula la derivada de:
- 6.
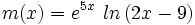
Calcula la derivada de y respecto de la variable t:
- 7.
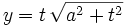
Calcula la derivada de:
- 8.
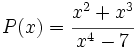
Calcula la derivada de:
- 9.
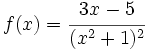
Calcula la derivada de:
- 10.
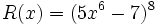
Calcula la derivada de:
- 11.
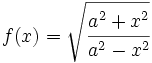
Calcula la derivada de:
- 12.
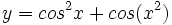
Calcula la derivada de:
- 13.
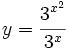
Calcula la derivada de:
- 14.
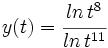
Calcula la derivada de:
- 15.
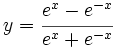
Calcula la derivada de:
- 16.
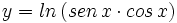
Calcula la derivada de:
- 17.
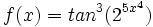
Calcula la derivada de:
- 18.
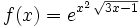
Calcula la derivada de:
- 19.
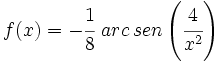
Calcula la derivada de:
- 20.
![f(x)=ln \left[\cfrac{(x+4)^2 (x-1)^3}{(x-7)^5}\right]](/wikipedia/images/math/e/c/d/ecde96d50c8ef6b266dbcf433955436a.png)
21. Sabiendo que f(2)=4, f'(4)=6 y f'(2)=-2, calcula:
- a)
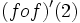
- b) La derivada de
![\left[ f(x) \right]^3](/wikipedia/images/math/5/6/c/56c8fcef02935697244f781072a5d5cc.png) cuando x=2.
cuando x=2.
Calcula la derivada de:
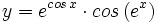
Calcula la derivada de:
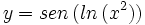
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
| Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
Calcula la derivada de:
|
Calcula la derivada de:
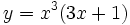
Calcula la derivada de:
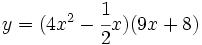
Calcula la derivada de:
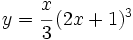
Calcula la derivada de:
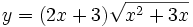
Calcula la derivada de:
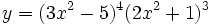
Calcula la derivada de:
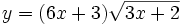
Calcula la derivada de:
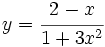
Calcula la derivada de:
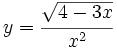
Calcula la derivada de:
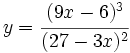
Calcula la derivada de: No se pudo entender (función desconocida\sqrtt): y=\cfrac{x\sqrtt{x+1}}{x+1}\;
Calcula la derivada de:
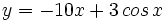
Calcula la derivada de:
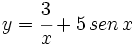
Calcula la derivada de:
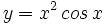
Calcula la derivada de:
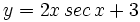
Calcula la derivada de:
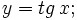
Calcula la derivada de:
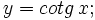
Calcula la derivada de:
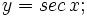
Calcula la derivada de:
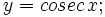
Calcula la derivada de:
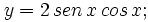
Calcula la derivada de:
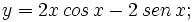
Calcula la derivada de:
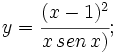
Estudio de la continuidad y de la derivabilidad de una función.
Videotutoriales para aprender a derivar.
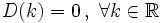
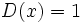
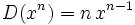
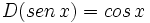
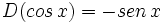
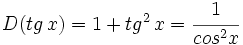
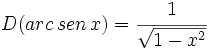
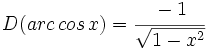
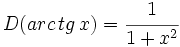
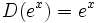
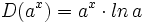
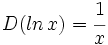
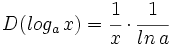
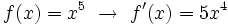
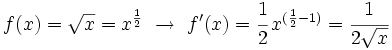
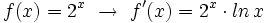
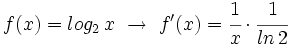
![D[k\,f(x)]=k\,f'(x)\;](/wikipedia/images/math/1/e/1/1e1df26b1290307dd9f35c29b3314606.png)
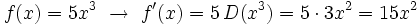
![D[f(x)+g(x)]=f'(x)+g'(x)\;](/wikipedia/images/math/5/d/7/5d79cbe9e2246a5e1ec6da9fbc79488a.png)
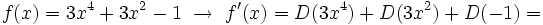
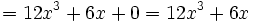
![D[f(x) \cdot g(x)]=f'(x) \cdot g(x) + f(x) \cdot g'(x)\;](/wikipedia/images/math/f/f/2/ff213fdc8e847b6f0297c2bfe5bc7bc9.png)
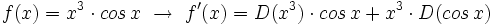
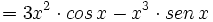
![D \left[ \cfrac{f(x)}{g(x)} \right]=\cfrac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g(x)^2}\;](/wikipedia/images/math/2/8/9/289dba05ff7161fe04e9c4f47e590aeb.png)
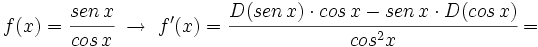
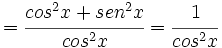
![D\{g[f(x)]\}=g'[f(x)] \cdot f'(x)\;](/wikipedia/images/math/8/c/0/8c0fc752c9b70aeceeb69e8db044064c.png)
![f(x)=sen^2 x \ \rightarrow \ f'(x)=2 \, sen \, x \cdot D[sen \, x]=2 \, sen \, x \cdot cos \, x](/wikipedia/images/math/c/e/0/ce09587b5cfe3fc619d1249a5774edbe.png)
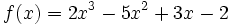
![g(x)=\sqrt{2x} + \sqrt[3]{5x^2}](/wikipedia/images/math/6/c/f/6cfa5409603bbccecaf9975cc3a521a5.png)
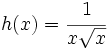
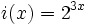
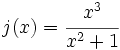
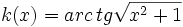
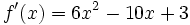
![g'(x)=\cfrac{\sqrt{2}}{2\sqrt{x}}+\cfrac{2\sqrt[3]{5}}{3\sqrt[3]{x}}](/wikipedia/images/math/1/6/b/16b48fc83d3329530c3d03d74b74267d.png)
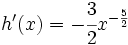
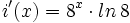
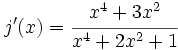
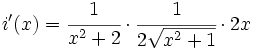
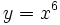
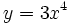
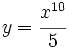
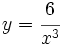
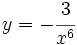
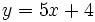
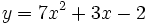
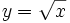
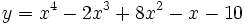
![y=\cfrac{\sqrt[3]{x}}{2}\;](/wikipedia/images/math/e/e/3/ee3ef885e772009899ee012d09f36797.png)
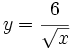
![y=\cfrac{5}{\sqrt[4]{x}}\;](/wikipedia/images/math/2/3/2/23296e2cda990bca628428358d68b3e2.png)
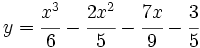
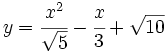
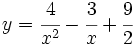
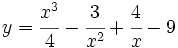
![y=\cfrac{\sqrt[3]{x}}{5}-\cfrac{2}{\sqrt[3]{x}}\;](/wikipedia/images/math/7/0/2/702e273a509597d8581217ff5ef668be.png)
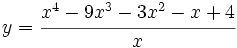
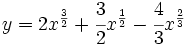
![y=4\sqrt{x}+3\sqrt[3]{x^2}+4\sqrt{x^3}\;](/wikipedia/images/math/7/e/f/7ef0ad404cf650fe31cd403c5d5597d6.png)
![y=\cfrac{2}{\sqrt[4]{x^3}}+\cfrac{1}{\sqrt[3]{x}}-\cfrac{3}{x^{-2}}\;](/wikipedia/images/math/9/e/2/9e20930a1bfb21f7beda49a80546b309.png)
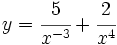
![y=\cfrac{3x^2+5x+8}{\sqrt[4]{x}}\;](/wikipedia/images/math/4/c/4/4c4e04184d25e1baf2fa223187922000.png)
![y=\left[(2x^4)^3 \right]^2+10x^3\;](/wikipedia/images/math/9/b/4/9b4e087a8c0407be2ab106bf7ceba4f8.png)