Límite de una función (2ºBach)
De Wikipedia
| Revisión de 07:33 22 jun 2017 Coordinador (Discusión | contribuciones) (→Límite de de una función en un punto) ← Ir a diferencia anterior |
Revisión de 07:36 22 jun 2017 Coordinador (Discusión | contribuciones) (→Límite de de una función en un punto) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Límite de de una función en un punto== | ==Límite de de una función en un punto== | ||
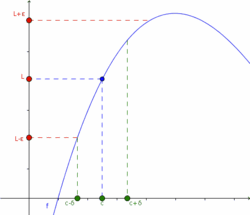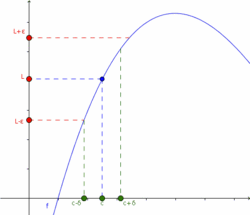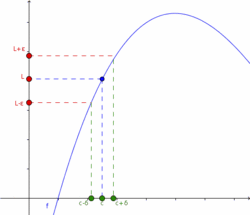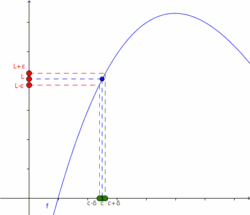
| - | [[Imagen:Limite01.png|thumb|250px|Visualización de los parámetros utilizados en la definición de límite.]] | + | {{Tabla50|celda2=[[Imagen:Limite01.png|thumb|center|250px|Visualización de los parámetros utilizados en la definición de límite.]] |
| - | El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto. | + | |celda1=El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto. |
| De manera informal, diremos que una función <math>f ~</math> tiene límite <math>L~</math> en <math>c~</math> , o que <math>f ~</math> tiende a <math>L ~</math> cuando x se acerca a <math>c ~</math> si se puede hacer que <math>f(x)~</math> esté tan cerca como queramos de <math>L ~</math> haciendo que <math>x~</math> esté suficientemente cerca de <math>c~</math>, siendo <math>x~</math> distinto de <math>c~</math>. | De manera informal, diremos que una función <math>f ~</math> tiene límite <math>L~</math> en <math>c~</math> , o que <math>f ~</math> tiende a <math>L ~</math> cuando x se acerca a <math>c ~</math> si se puede hacer que <math>f(x)~</math> esté tan cerca como queramos de <math>L ~</math> haciendo que <math>x~</math> esté suficientemente cerca de <math>c~</math>, siendo <math>x~</math> distinto de <math>c~</math>. | ||
| - | + | }} | |
| Los conceptos ''cerca'' y ''suficientemente cerca'' son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice: | Los conceptos ''cerca'' y ''suficientemente cerca'' son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice: | ||
| Línea 19: | Línea 19: | ||
| Esto, escrito en notación formal: | Esto, escrito en notación formal: | ||
| - | <math>\lim_{x\to c} \, \,f(x) = L</math><math>\iff \forall \varepsilon > 0 ,\,\,\, \exists \delta > 0 \, \ | \ \, \forall x \in \operatorname{Dom}(f), \,\,0<|x-c|<\delta \rightarrow |f(x)-L|<\varepsilon | + | <center><math>\lim_{x\to c} \, \,f(x) = L</math><math>\iff \forall \varepsilon > 0 ,\,\,\, \exists \delta > 0 \, \ | \ \, \forall x \in \operatorname{Dom}(f), \,\,0<|x-c|<\delta \rightarrow |f(x)-L|<\varepsilon |
| - | </math> | + | </math></center> |
| }} | }} | ||
| [[Imagen:Limite02.gif|thumb|250px|Tomando valores arbitrarios de ''ε'', podemos elegir un δ para cada uno de estos, de modo que ''f''(''x'') y ''L'' se acerquen a medida que ''x'' se acerca a ''c''.]] | [[Imagen:Limite02.gif|thumb|250px|Tomando valores arbitrarios de ''ε'', podemos elegir un δ para cada uno de estos, de modo que ''f''(''x'') y ''L'' se acerquen a medida que ''x'' se acerca a ''c''.]] | ||
Revisión de 07:36 22 jun 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Límite de de una función en un punto
| El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
De manera informal, diremos que una función |
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función  , cuando
, cuando 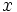 tiende a
tiende a 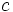 , es
, es 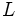 , si y sólo si, para todo
, si y sólo si, para todo 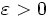 , existe un
, existe un 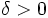 , tal que para todo número real
, tal que para todo número real 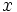 en el dominio de la función, si
en el dominio de la función, si 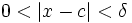 entonces
entonces 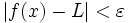 .
.
Esto, escrito en notación formal:
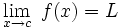
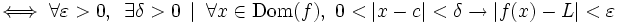
Esta es una formulación estricta del concepto de límite de una función real en un punto de acumulación del dominio de la función y se debe al matemático francés Luis Cauchy.
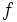 tiene límite
tiene límite 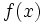 esté tan cerca como queramos de
esté tan cerca como queramos de