Punto de acumulación
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:37 23 jun 2017 Coordinador (Discusión | contribuciones) (→Punto de acumulación en el conjunto de los números reales) ← Ir a diferencia anterior |
Revisión de 08:44 23 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Punto de acumulación en el conjunto de los números reales== | ==Punto de acumulación en el conjunto de los números reales== | ||
| - | {{Caja_Amarilla|texto=Sea <math>S\;</math> un subconjunto de <math>\mathbb{R}</math>. Un punto <math>x \in \mathbb{R}</math> es un '''punto de acumulación''' de <math>S\;</math> si cualquier intervalo abierto que contenga a <math>x\;</math> contiene algún punto de <math>S\;</math> distinto de <math>x\;</math>. | + | {{Caja_Amarilla|texto=*Sea <math>S\;</math> un subconjunto de <math>\mathbb{R}</math>. Un punto <math>x \in \mathbb{R}</math> es un '''punto de acumulación''' de <math>S\;</math> si cualquier intervalo abierto que contenga a <math>x\;</math> contiene algún punto de <math>S\;</math> distinto de <math>x\;</math>. También se denomina '''punto de contacto''', '''punto límite''' o '''punto de aglomeración'''. |
| - | Un punto de acumulación también se denomina '''punto de contacto''', '''punto límite''' o '''punto de aglomeración'''.}} | + | *De manera intuitiva, </math><math>x \in \mathbb{R}</math> es un punto de acumulación de </math><math>S\;</math>, si puede ser aproximado por puntos de <math>S\;</math> distintos a <math>x\;</math> tanto como se desee. |
| + | |||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
Revisión de 08:44 23 jun 2017
Punto de acumulación en el conjunto de los números reales
- Sea
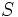 un subconjunto de
un subconjunto de  . Un punto
. Un punto 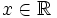 es un punto de acumulación de
es un punto de acumulación de 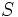 si cualquier intervalo abierto que contenga a
si cualquier intervalo abierto que contenga a  contiene algún punto de
contiene algún punto de 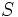 distinto de
distinto de  . También se denomina punto de contacto, punto límite o punto de aglomeración.
. También se denomina punto de contacto, punto límite o punto de aglomeración.
- De manera intuitiva, </math>
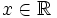 es un punto de acumulación de </math>
es un punto de acumulación de </math>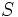 , si puede ser aproximado por puntos de
, si puede ser aproximado por puntos de 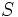 distintos a
distintos a  tanto como se desee.
tanto como se desee.
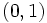 tiene como puntos de acumulación a todos los puntos del intervalo
tiene como puntos de acumulación a todos los puntos del intervalo ![[0,1]\;](/wikipedia/images/math/0/c/c/0ccfe73327271e91a28e86855315af81.png) .
.
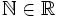 no tiene puntos de acumulación. En general, cualquier subconjunto finito de
no tiene puntos de acumulación. En general, cualquier subconjunto finito de 
