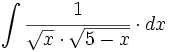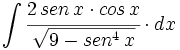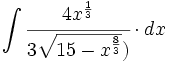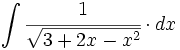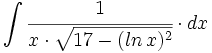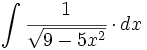Cálculo de primitivas inmediatas (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 06:34 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:37 26 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 101: | Línea 101: | ||
| #<math>\int \cfrac{\sqrt[4]{1+cotg \, 3x}}{sen^2 \, 3x} \cdot dx</math> | #<math>\int \cfrac{\sqrt[4]{1+cotg \, 3x}}{sen^2 \, 3x} \cdot dx</math> | ||
| #Determine la función "f" tal que: f(0)=0, f'(0)=5, f''(0)=1 y f'''(x)=x+1 | #Determine la función "f" tal que: f(0)=0, f'(0)=5, f''(0)=1 y f'''(x)=x+1 | ||
| - | #Determine la primitiva de <math>f(x)=sen \, x \cdot cos \,x /math> que pasa por el origen. | + | #Determine la primitiva de <math>f(x)=sen \, x \cdot cos \,x </math> que pasa por el origen. |
| + | |||
| |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-integral/01-calculo-de-primitivas-2/050107-seis-ejercicios-2 | |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-integral/01-calculo-de-primitivas-2/050107-seis-ejercicios-2 | ||
| }} | }} | ||
Revisión de 06:37 26 jun 2017
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Ejercicios resueltos: Primitivas inmediatas
Primitivas del tipo ![\int [u(x)]^m \cdot u'(x) \cdot dx \quad (m \ne -1)](/wikipedia/images/math/d/0/b/d0b6088fa26b6d625de05c0a40b70602.png)
- Primitivas del tipo
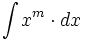
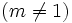 . Ejemplos
. Ejemplos
- Ejercicios:
- Primitivas del tipo
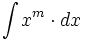
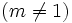 en las que hay que aplicar el binomio de Newton.
en las que hay que aplicar el binomio de Newton.
- Ejercicios:
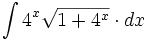
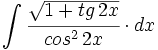
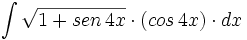
![\int \cfrac{\sqrt[4]{1+cotg \, 3x}}{sen^2 \, 3x} \cdot dx](/wikipedia/images/math/8/f/2/8f234b8b662cc63a891d726b7da2ec0c.png)
- Determine la función "f" tal que: f(0)=0, f'(0)=5, f(0)=1 y f'(x)=x+1
- Determine la primitiva de
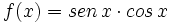 que pasa por el origen.
que pasa por el origen.
Ejercicios resueltos: Primitivas inmediatas
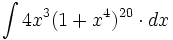
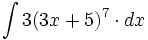
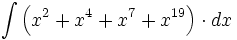
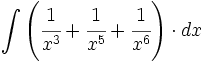
![\int \left( \sqrt{x} + \sqrt[3]{x} + \sqrt[6]{x} + \sqrt[8]{x}\right) \cdot dx](/wikipedia/images/math/a/d/7/ad7b72d3dc41c911a4cf21a1642eeead.png)
![\int \left( \cfrac{1}{\sqrt[5]{x}} + \cfrac{1}{\sqrt[7]{x}} + \cfrac{1}{\sqrt[9]{x}}\right) \cdot dx](/wikipedia/images/math/6/4/7/6472b81d1d67dc15b37e43230a2dd291.png)
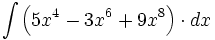
![\int \left( 5 -3\sqrt{x}+9\sqrt[5]{x} \right) \cdot dx](/wikipedia/images/math/8/a/9/8a9fe9ee2f33c419cf96dc0ee568039f.png)
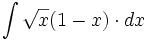
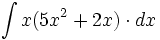
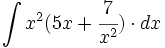
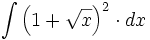
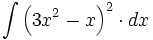
![\int \left( 2+ \sqrt[3]{x} \right)^3 \cdot dx](/wikipedia/images/math/4/1/4/414d418a1a496473d75f833b5d26fc12.png)
![\int \left( 2- \sqrt[3]{x} \right)^3 \cdot dx](/wikipedia/images/math/a/4/4/a4489d3417128570c75d0ec26f905bf9.png)
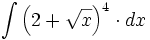
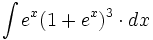
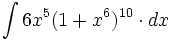
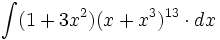
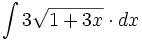
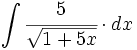
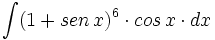
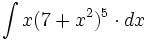
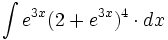
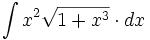
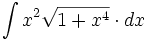
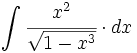
![\int \cfrac{1}{x\sqrt[4]{1-ln \, x}} \cdot dx](/wikipedia/images/math/c/f/c/cfc07daf2baefd842e5848f0f7e03f42.png)
![\int \cfrac{sen \, 3x}{\sqrt[5]{1-cos \, 3x}} \cdot dx](/wikipedia/images/math/f/e/d/fedd75fa6e1b4fc832a1b3244d31d706.png)
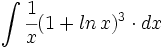
![\int \cfrac{7}{\sqrt[3]{1+7x}} \cdot dx](/wikipedia/images/math/3/e/c/3ec4553d16d4a020caac805f5621e032.png)
![\int 2\sqrt[3]{1+2x} \cdot dx](/wikipedia/images/math/9/1/9/919dbc3b549d0ed508a6e32d4f1eb63f.png)
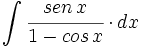
![\int \cfrac{cos \, x}{\sqrt[3]{1+sen \, x}} \cdot dx](/wikipedia/images/math/7/1/d/71d9e7ee213b836b85f2bed8530bad51.png)
![\int \cfrac{1}{x\sqrt[4]{1+ln \, x}} \cdot dx](/wikipedia/images/math/3/6/e/36e712c3e51f2f00db9567790cce7502.png)
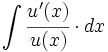
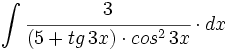
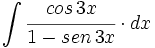
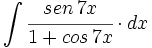
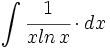
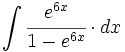
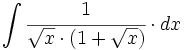
![\int \cfrac{1}{\sqrt[3]{x} \cdot (1+\sqrt[3]{x^2})} \cdot dx](/wikipedia/images/math/e/0/0/e00ec3c06bca7273fafc77dfb13d2365.png)
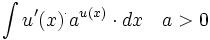
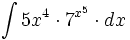
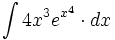
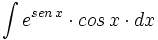
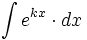
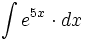
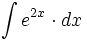
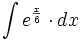
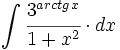
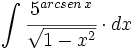
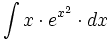
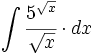
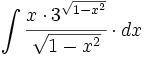
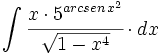
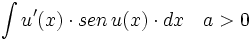
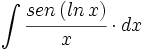
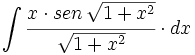
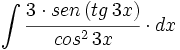
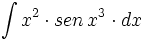
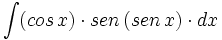
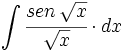
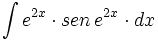
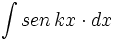
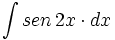
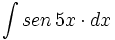
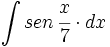
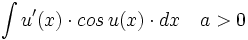
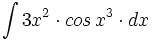
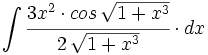
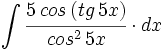
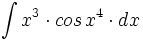
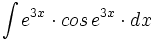
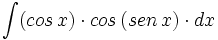
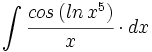
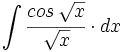
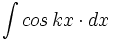
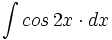
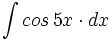
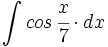
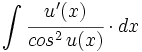
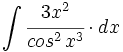
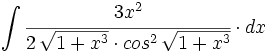
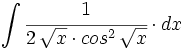
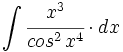
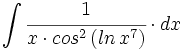
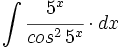
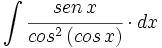
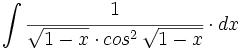
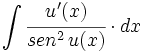
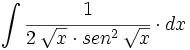

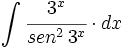
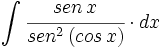
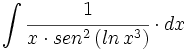
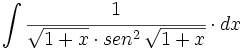
![\int \cfrac{u'(x)}{a^2+[u(x)]^2} \cdot dx](/wikipedia/images/math/1/2/1/1216aad7e7c8189456878755ca0c846c.png)
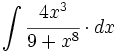
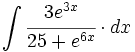
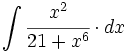
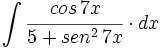
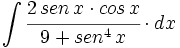
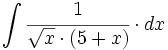
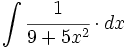
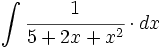
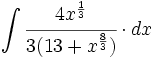
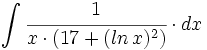
![\int \cfrac{u'(x)}{\sqrt{a^2-[u(x)]^2}} \cdot dx](/wikipedia/images/math/7/0/e/70e26d7ca7ea8762b35e39fea301f6a4.png)