Plantilla:Def fraccion
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 15:32 20 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:27 27 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| *El numero <math>a\;\!</math> se llama '''numerador''' e indica las partes que tomamos de dicha división.}} | *El numero <math>a\;\!</math> se llama '''numerador''' e indica las partes que tomamos de dicha división.}} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Las fracciones | ||
| + | |duracion=13'06" | ||
| + | |sinopsis= | ||
| + | *Definición de fracción. | ||
| + | *Fracciones equivalentes. | ||
| + | *Simplificación de fracciones. Fracciones irreducibles. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=cJ6fB50Cw10&list=PL773F27163628CA1F&index=3 | ||
| + | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| |titulo1=Clasificación de las fracciones | |titulo1=Clasificación de las fracciones | ||
Revisión de 11:27 27 jun 2017
Una fracción es es la expresión de una cantidad dividida entre otra cantidad; es decir que representa un cociente no efectuado de números.
Se representa de la forma 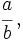 con
con 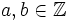
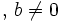 . También se puede representar
. También se puede representar 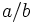 .
.
- El número
 se llama denominador e indica las partes iguales en que se divide la unidad.
se llama denominador e indica las partes iguales en que se divide la unidad.
- El numero
 se llama numerador e indica las partes que tomamos de dicha división.
se llama numerador e indica las partes que tomamos de dicha división.
- Definición de fracción.
- Fracciones equivalentes.
- Simplificación de fracciones. Fracciones irreducibles.
Clasificación de las fracciones:
- Fracciones propias e impropias.
- Fracciones ordinarias y decimales.
- Fracciones homogeneas y heterogeneas.
- Fracciones irreducibles y reducibles.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según el valor las fracciones pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.

