Plantilla:Videos: Distancia entre dos puntos del plano
De Wikipedia
| Revisión de 11:15 18 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 19: | Línea 19: | ||
| |sinopsis=Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos. | |sinopsis=Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos. | ||
| |url1=https://www.youtube.com/watch?v=ZPR5WeYv3B4&list=PLHwz3md30-3kyfZgB4y53rPmPydQwj6uj&index=3 | |url1=https://www.youtube.com/watch?v=ZPR5WeYv3B4&list=PLHwz3md30-3kyfZgB4y53rPmPydQwj6uj&index=3 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 4 | ||
| + | |duracion=10'06" | ||
| + | |sinopsis=*Fórmula de la distancia euclidea entre dos puntos del plano. Ejemplos. | ||
| + | *Otra distancia: la "distancia de Manhattan". | ||
| + | |url1=https://www.youtube.com/watch?v=PsXbOKgPHmg&index=2&list=PL811F7AF8E8EC9655 | ||
| }} | }} | ||
| ---- | ---- | ||
| Línea 50: | Línea 57: | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| |duracion=4'49" | |duracion=4'49" | ||
| - | |sinopsis=Halla la distancia entre los puntos <math>A(\cfrac{-\sqrt{5}}{4},\cfrac{3}{5})\;</math> y <math>B(\cfrac{\sqrt{5}}{4},-\cfrac{1}{5})\;</math>. | + | |sinopsis=Halla la distancia entre los puntos <math>A \left( \cfrac{-\sqrt{5}}{4},\cfrac{3}{5}\right)\;</math> y <math>B \left(\cfrac{\sqrt{5}}{4},-\cfrac{1}{5}\right)\;</math>. |
| |url1=https://www.youtube.com/watch?v=_7PwNmGPdQc&index=5&list=PLo7_lpX1yruPQnc8UTz9H_JKkhqvJa1RV | |url1=https://www.youtube.com/watch?v=_7PwNmGPdQc&index=5&list=PLo7_lpX1yruPQnc8UTz9H_JKkhqvJa1RV | ||
| }} | }} | ||
| Línea 91: | Línea 98: | ||
| |sinopsis=La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P. | |sinopsis=La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P. | ||
| |url1=https://www.youtube.com/watch?v=-Lh6p6yM5dk&list=PLo7_lpX1yruOtTggg_l_Id2KGuSHgx7Hi&index=6 | |url1=https://www.youtube.com/watch?v=-Lh6p6yM5dk&list=PLo7_lpX1yruOtTggg_l_Id2KGuSHgx7Hi&index=6 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=6'15" | ||
| + | |sinopsis=Sean los puntos M(5,2) y N(1,k). Determina "k" en cada uno de los siguientes casos: | ||
| + | |||
| + | a) d(M,N)=4;{{b4}}b) d(M,N)=6;{{b4}}c) d(M,N)=1 | ||
| + | |url1=https://www.youtube.com/watch?v=rlTArn74NDo&list=PL811F7AF8E8EC9655&index=4 | ||
| }} | }} | ||
| ---- | ---- | ||
| Línea 96: | Línea 111: | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 7 | + | |titulo1=Ejercicio 1 |
| |duracion=6'21" | |duracion=6'21" | ||
| |sinopsis=Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1). | |sinopsis=Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1). | ||
| Línea 102: | Línea 117: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 8 | + | |titulo1=Ejercicio 2 |
| |duracion=6'21" | |duracion=6'21" | ||
| |sinopsis=Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1). | |sinopsis=Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1). | ||
| Línea 108: | Línea 123: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 9 | + | |titulo1=Ejercicio 3 |
| |duracion=9'17" | |duracion=9'17" | ||
| |sinopsis=Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón. | |sinopsis=Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón. | ||
| Línea 114: | Línea 129: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 10 | + | |titulo1=Ejercicio 4 |
| |duracion=9'17" | |duracion=9'17" | ||
| |sinopsis=Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón. | |sinopsis=Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón. | ||
| Línea 120: | Línea 135: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 11 | + | |titulo1=Ejercicio 5 |
| |duracion=7'56" | |duracion=7'56" | ||
| |sinopsis=Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área. | |sinopsis=Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área. | ||
| Línea 126: | Línea 141: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 12 | + | |titulo1=Ejercicio 6 |
| |duracion=8'04" | |duracion=8'04" | ||
| |sinopsis=Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área. | |sinopsis=Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área. | ||
| Línea 132: | Línea 147: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 13 | + | |titulo1=Ejercicio 7 |
| |duracion=5'46" | |duracion=5'46" | ||
| |sinopsis=Verifica que los puntos <math>A(-1,0)\;</math>, <math>B(3,0)\;</math> y <math>C(1,2\sqrt{3})</math> forman un triángulo equilátero. | |sinopsis=Verifica que los puntos <math>A(-1,0)\;</math>, <math>B(3,0)\;</math> y <math>C(1,2\sqrt{3})</math> forman un triángulo equilátero. | ||
| Línea 138: | Línea 153: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 14 | + | |titulo1=Ejercicio 8 |
| |duracion=6'04" | |duracion=6'04" | ||
| |sinopsis=Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles. | |sinopsis=Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles. | ||
| |url1=https://www.youtube.com/watch?v=S4ESR26Arx8&list=PLo7_lpX1yruMiWllMi2gSp6kQ1Rge8ajj&index=4 | |url1=https://www.youtube.com/watch?v=S4ESR26Arx8&list=PLo7_lpX1yruMiWllMi2gSp6kQ1Rge8ajj&index=4 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=7'54" | ||
| + | |sinopsis=Analizar si el triángulo A(7,3), B(1,-4) y C(3,5) es equilátero. | ||
| + | |url1=https://www.youtube.com/watch?v=vjhiCA-nF_A&index=3&list=PL811F7AF8E8EC9655 | ||
| }} | }} | ||
| ---- | ---- | ||
| Línea 147: | Línea 168: | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 15 | + | |titulo1=Ejercicio 1 |
| |duracion=6´12" | |duracion=6´12" | ||
| |url1=https://www.youtube.com/watch?v=XWf2aTgZnKo&index=1&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm | |url1=https://www.youtube.com/watch?v=XWf2aTgZnKo&index=1&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm | ||
| Línea 153: | Línea 174: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 16 | + | |titulo1=Ejercicio 2 |
| |duracion=6´11" | |duracion=6´11" | ||
| |url1=https://www.youtube.com/watch?v=BHSCLoW-kA0&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=2 | |url1=https://www.youtube.com/watch?v=BHSCLoW-kA0&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=2 | ||
| Línea 159: | Línea 180: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 17 | + | |titulo1=Ejercicio 3 |
| |duracion=8´12" | |duracion=8´12" | ||
| |url1=https://www.youtube.com/watch?v=og2G0zmxnSk&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=3 | |url1=https://www.youtube.com/watch?v=og2G0zmxnSk&list=PLo7_lpX1yruNRHTd8WJ1qVUk5zgHURBGm&index=3 | ||
| |sinopsis=Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias. | |sinopsis=Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias. | ||
| + | }} | ||
| + | ---- | ||
| + | Otros: | ||
| + | |||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=7'30" | ||
| + | |sinopsis=Determina los puntos del plano cuya distancia al punto M(3,-5) sea 2. | ||
| + | |url1=https://www.youtube.com/watch?v=1da8uIHMgrQ&index=5&list=PL811F7AF8E8EC9655 | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
- Módulo de un vector = distancia entre dos puntos. Demostración de la fórmula.
- Ejemplos y ejercicios.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
- Fórmula de la distancia euclidea entre dos puntos del plano. Ejemplos.
- Otra distancia: la "distancia de Manhattan".
Cálculo de distancias:
Halla la distancia entre los puntos A(7,3) y B(3,-1).
Halla la distancia entre los puntos A(3,1/2) y B(4/3,-1).
Halla la distancia entre los puntos A(3/2,-1/6) y B(-1/2,1/3).
Halla la distancia entre los puntos 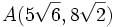 y
y 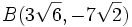 .
.
Halla la distancia entre los puntos 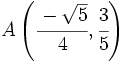 y
y 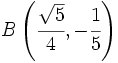 .
.
Halla la coordenada que falta:
Halla el valor de "x" para que la distancia entre los puntos A(x,-1) y B(9,4) sea 13.
Halla el valor de "y" para que la distancia entre los puntos P(7,1) y Q(3,y) sea 5.
Halla el punto Q el eje Y que equidista de A(4,2) y B(5,5).
Halla el punto P el eje X que equidista de A(5,1) y B(0,6).
Halla el punto P que equidista de A(7,-3), B(8,-2) y C(0,-2).
La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P.
Sean los puntos M(5,2) y N(1,k). Determina "k" en cada uno de los siguientes casos:
a) d(M,N)=4; b) d(M,N)=6; c) d(M,N)=1
Polígonos:
Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1).
Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1).
Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón.
Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón.
Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos 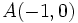 ,
, 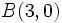 y
y 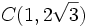 forman un triángulo equilátero.
forman un triángulo equilátero.
Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles.
Analizar si el triángulo A(7,3), B(1,-4) y C(3,5) es equilátero.
Puntos colineales:
Determina si los puntos A(-3,1), B(0,2) y C(6,4) son colineales, usando distancias.
Determina si los puntos A(321), B(0,0) y C(9,6) son colineales, usando distancias.
Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias.
Otros:
Determina los puntos del plano cuya distancia al punto M(3,-5) sea 2.

