Aplicaciones de la derivada (2ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 05:18 27 jun 2017
Coordinador (Discusión | contribuciones)
(→Utilidad de la segunda derivada)
← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)
(→Concavidad y puntos de inflexión)
Línea 10: Línea 10:
==Utilidad de la segunda derivada== ==Utilidad de la segunda derivada==
 +===Concavidad y puntos de inflexión===
 +{{Caja_Amarilla|texto=*Una función es '''cóncava''' (o '''concava hacia abajo''') en un intervalo (a,c), si para todo punto "b" del intervalo la recta tangente en ese punto queda por encima de la función.
 +*Una función es '''convexa''' (o '''concava hacia arriba''') en un intervalo (a,c), si para todo punto "b" del intervalo la recta tangente en ese punto queda por debajo de la función.
 +*Un '''punto de infexión''' de una función es aquel punto del dominio de la función en el cual la función cambia de concavidad, es decir, pasa de ser concava a convexa o viceversa.
 +}}{{p}}
 +{{Tabla50|celda1=[[Imagen:concava.png|300px|center]]{{p}}<center>Cóncava</center>|celda2=[[Imagen:convexa.png|300px|center]]{{p}}<center>Convexa</center>}}
 +{{p}}
 +{{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para estudiar la concavidad de una función deberemos estudiar el signo de la función derivada segunda:
 +
 +*En aquellos puntos donde la derivada segunda sea positiva la función será cóncava hacia arriba.
 +*En aquellos puntos donde la derivada segunda sea negativa la función será cóncava hacia abajo.
 +*En aquellos puntos donde la derivada segunda sea nula la función puede tener un punto de inflexión. Su determinación se hará viendo el signo de la derivada segunda antes y después del punto.
 +
 +}}
 +
{{Utilidad de la segunda derivada}} {{Utilidad de la segunda derivada}}
{{p}} {{p}}
 +
 +==Teoremas de Rolle, Lagrange y Cauchy==
 +{{Video_enlace_fonemato
 +|titulo1=Teorema de Rolle. Teorema de Lagrange
 +|duracion=20'03"
 +|sinopsis=
 +*00.00 - Introducción.
 +*05:15 - Teorema de Rolle.
 +*13:00 - Teorema de Lagrange.
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/25-teorema-de-rolle-teorema-de-lagrange-2
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Teorema de Cauchy
 +|duracion=9'29"
 +|sinopsis=Una generalización del teorema de Lagrange.
 +
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/26-teorema-de-cauchy-2
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Ejercicio 1
 +|duracion=2'35"
 +|sinopsis=Prueba que <math>f(x)=|x-1|\;</math> no verifica el teorema de Rolle en el intervalo [-2,0].
 +
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/002-ejercicio-7
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Ejercicio 2
 +|duracion=4'29"
 +|sinopsis=Aplicando el teorema de Lagrange a <math>f(x)= \sqrt{x}\;</math>, demostrar que <math>\cfrac{1}{9} < \sqrt{66} - 8 < \cfrac{1}{8}</math>.
 +
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/003-ejercicio-7
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Ejercicio 3
 +|duracion=1'51"
 +|sinopsis=Si <math>f(x)= 3+(x+1)^3 \cdot (x-2)^2\;</math>, ¿tiene f'(x)=0 alguna solución en el intervalo (-1,2)?
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/013-ejercicio-6
 +}}
 +{{Video_enlace_fonemato
 +|titulo1=Ejercicio 4
 +|duracion=2'51"
 +|sinopsis=Comprueba si <math>f:[0,2\pi] \rightarrow \mathbb{R}</math>, tal que <math>f(x)= 2x+sen \, x\;</math> cumple las hipótesis del teorema de Lagrange, y determina los puntos a los que hace referencia dicho teorema.
 +|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/019-ejercicio-4
 +}}
 +
==Ejercicios== ==Ejercicios==
{{Ejercicios: aplicacion derivada}} {{Ejercicios: aplicacion derivada}}
{{p}} {{p}}
[[Categoría: Matemáticas]][[Categoría: Funciones]] [[Categoría: Matemáticas]][[Categoría: Funciones]]

Revisión actual

Menú:
Enlaces internos Para repasar o ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Calculadora

Tabla de contenidos

[editar]

Estudio del crecimiento y de los puntos singulares

ejercicio

Procedimiento

Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:

  • En aquellos puntos donde la derivada sea positiva la función será creciente.
  • En aquellos puntos donde la derivada sea negativa la función será decreciente.

video
Estudio del crecimiento
Tutorial 1a (13'02")     Sinopsis:

Funciones crecientes y decrecientes

Tutorial 1b (7'19")     Sinopsis:

Criterios de crecimiento y decrecimiento

Ejercicio 1a (2'55")     Sinopsis:

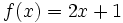
Estudia el crecimiento de f(x)=2x+1\;

Ejercicio 1b (4'01")     Sinopsis:

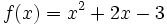
Estudia el crecimiento de f(x)=x^2+2x-3\;

Ejercicio 1c (8'31")     Sinopsis:

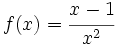
Estudia el crecimiento de f(x)=\cfrac{x-1}{x^2}\;

Ejercicio 2 (3'10")     Sinopsis:

Demuestra que 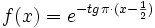f(x)=e^{-tg \, \pi \cdot (x-\frac{1}{2})} es positiva y decreciente en el intervalo (0,1).

Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.

Esos puntos pueden ser puntos extremos (máximos o mínimos), pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.

video
Extremos de una función
Tutorial 1a (11'58")     Sinopsis:

Monotonía y extremos relativos

Tutorial 1b (17'13")     Sinopsis:

Monotonía y extremos relativos.Ejemplos

Tutorial 2 (23'32")     Sinopsis:

¿Qué son los puntos máximos, mínimos, locales y globales, crecimiento y decrecimiento?

Tutorial 3a (13'46")     Sinopsis:

Determinación de los extremos relativos

Tutorial 3b (14'45")     Sinopsis:

Determinación de máximos y mínimos absolutos

Ejercicio 1 (9'04")     Sinopsis:

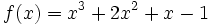
Estudia el crecimiento y los puntos extremos de f(x)=x^3+2x^2+x-1\;

Ejercicio 2a (13'12")     Sinopsis:

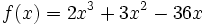
Estudia el crecimiento y los puntos extremos de f(x)=2x^3+3x^2-36x\;

Ejercicio 2b (11'57")     Sinopsis:

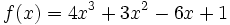
Estudia el crecimiento y los puntos extremos de f(x)=4x^3+3x^2-6x+1\;

Ejercicio 2c (11'34")     Sinopsis:

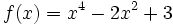
Estudia el crecimiento y los puntos extremos de f(x)=x^4-2x^2+3\;

Ejercicio 2d (6'49")     Sinopsis:

Halla los máximos y mínimos de 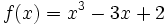f(x)=x^3-3x+2\;

Ejercicio 2e (7'42")     Sinopsis:

Encuentra el valor de "k" tal que 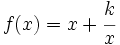f(x)=x+\cfrac{k}{x}\; tenga un máximo local en x=-2.

Ejercicio 3a (4'58")     Sinopsis:

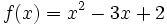
Halla los máximos y mínimos de f(x)=x^2-3x+2\;

Ejercicio 3b (8'11")     Sinopsis:

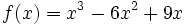
Halla los máximos y mínimos de f(x)=x^3-6x^2+9x\;

Ejercicio 3c (9'43")     Sinopsis:

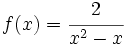
Halla los máximos y mínimos de f(x)=\cfrac{2}{x^2-x}\;

Ejercicio 3d (7'52")     Sinopsis:

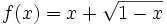
Halla los máximos y mínimos de f(x)=x+\sqrt{1-x}\;

Ejercicio 3e (7'02")     Sinopsis:

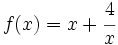
Halla los máximos y mínimos de f(x)=x+\cfrac{4}{x}\;

ejercicio

Ejercicio resuelto: Puntos singulares y crecimiento

Dada la función 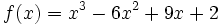f(x)=x^3-6x^2+9x+2\;, halla sus puntos singulares y estudia su crecimiento.

Solución:

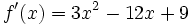
f'(x)=3x^2-12x+9\;

Puntos singulares:

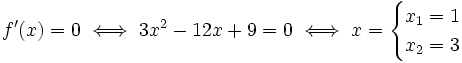
f'(x)=0 \iff 3x^2-12x+9=0 \iff x=\begin{cases} x_1= 1 \\ x_2=3 \end{cases}

Para estudiar el crecimiento determinaremos el signo de la función derivada mediante una tabla en la que estableceremos zonas delimitadas por los puntos singulares y por los puntos de discontinuidad, si los hubiese. En nuestro caso hay 3 zonas porque hay 2 puntos singulares y no hay discontinuidades, por tratarse f'(x) de una función polinómica. 

             -inf     1       3    +inf       
          -----!------!-------!------!
          f'(x)!  +   !   -   !  +   !
          -----!------!-------!------!
           f(x)! Cre  ! Decre ! Cre  !
          ----------------------------
Como f(1)=6 y f(3)=2, el anterior análisis del crecimiento nos permite determinar que (1,6) es un máximo y (3,2) es un mínimo.

wolfram
Extremos relativos
wolfram

Actividad: Extremos relativos

Nota para los cursos de secundaria: Algunas de las siguientes actividades son sólo ilustrativas ya que su resolución manual requiere conocimientos de 1º de bachillerato.

a) Halla los máximos relativos de la función y=x(40-x)\;
b) Halla los mínimos relativos de la función y=x^2+2x+1\;
c) Halla los extremos relativos (máximos y mínimos relativos) de la función y=\cfrac{x^3}{3}-x^2-8x\;.

Solución:
Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
a) maxima x(40-x)
b) minima x^2+2x+1
c) extrema x^3/3-x^2-8x


[editar]

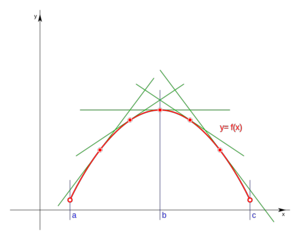
Utilidad de la segunda derivada

[editar]

Concavidad y puntos de inflexión

  • Una función es cóncava (o concava hacia abajo) en un intervalo (a,c), si para todo punto "b" del intervalo la recta tangente en ese punto queda por encima de la función.
  • Una función es convexa (o concava hacia arriba) en un intervalo (a,c), si para todo punto "b" del intervalo la recta tangente en ese punto queda por debajo de la función.
  • Un punto de infexión de una función es aquel punto del dominio de la función en el cual la función cambia de concavidad, es decir, pasa de ser concava a convexa o viceversa.

Cóncava

Convexa

ejercicio

Procedimiento

Para estudiar la concavidad de una función deberemos estudiar el signo de la función derivada segunda:

  • En aquellos puntos donde la derivada segunda sea positiva la función será cóncava hacia arriba.
  • En aquellos puntos donde la derivada segunda sea negativa la función será cóncava hacia abajo.
  • En aquellos puntos donde la derivada segunda sea nula la función puede tener un punto de inflexión. Su determinación se hará viendo el signo de la derivada segunda antes y después del punto.


Derivadas de orden superior (16'51")     Sinopsis:
video
Utilidad de la segunda derivada
Concavidad y puntos de inflexión (30'41")     Sinopsis:

Concavidad:

Ejercicio 1 (2'44")     Sinopsis:

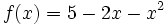Estudia la concavidad de f(x)=5-2x-x^2\;.

Ejercicio 2 (5'20")     Sinopsis:

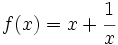Estudia la concavidad de f(x)=x+\cfrac{1}{x}.

Ejercicio 3 (8'28")     Sinopsis:

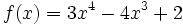Estudia la concavidad de f(x)=3x^4-4x^3+2\;.

Puntos de inflexión:

Ejercicio 1 (4'07")     Sinopsis:

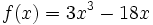Estudia la concavidad de f(x)=3x^3-18x\;.

Ejercicio 2 (11'24")     Sinopsis:

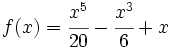Estudia la concavidad de f(x)=\cfrac{x^5}{20}-\cfrac{x^3}{6}+x.

Ejercicio 3 (7'02")     Sinopsis:

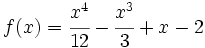Estudia la concavidad de f(x)=\cfrac{x^4}{12}-\cfrac{x^3}{3}+x-2.

Ejercicio 4 (7'30")     Sinopsis:

Hallar "a", "b" y "c" para que la función 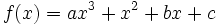f(x)=ax^3+x^2+bx+c\; tenga un máximo relativo en (0,3) y un punto de inflexión en x=1.

Máximos y mínimos (usando f "):

Ejercicio 1 (5'16")     Sinopsis:

Estudia los máximos y mínimos de 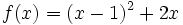f(x)=(x-1)^2+2x\;.

Ejercicio 2 (9'04")     Sinopsis:

Estudia los máximos y mínimos de No se pudo entender (función desconocida\cfac): f(x)=\cfac{1}{3}x^3-x\; .

Ejercicio 3 (8'59")     Sinopsis:

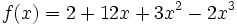Estudia los máximos y mínimos de f(x)=2+12x+3x^2-2x^3\;.

Ejercicio 4 (5'33")     Sinopsis:

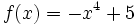Estudia los máximos y mínimos de f(x)=-x^4+5\;.

Ejercicio 5 (16'49")     Sinopsis:

Estudia los máximos y mínimos de No se pudo entender (función desconocida\cfac): f(x)=\cfac{x^2-3}{x^3}\; .

[editar]

Teoremas de Rolle, Lagrange y Cauchy

Teorema de Rolle. Teorema de Lagrange (20'03")     Sinopsis:
  • 00.00 - Introducción.
  • 05:15 - Teorema de Rolle.
  • 13:00 - Teorema de Lagrange.
Teorema de Cauchy (9'29")     Sinopsis:

Una generalización del teorema de Lagrange.

Ejercicio 1 (2'35")     Sinopsis:

Prueba que 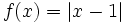f(x)=|x-1|\; no verifica el teorema de Rolle en el intervalo [-2,0].

Ejercicio 2 (4'29")     Sinopsis:

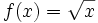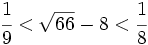Aplicando el teorema de Lagrange a f(x)= \sqrt{x}\;, demostrar que \cfrac{1}{9} < \sqrt{66} - 8 < \cfrac{1}{8}.

Ejercicio 3 (1'51")     Si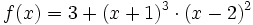nopsis:

Si f(x)= 3+(x+1)^3 \cdot (x-2)^2\;, ¿tiene f'(x)=0 alguna solución en el intervalo (-1,2)?

Ejercicio 4 (2'51")     Sinopsis:

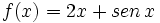Comprueba si f:[0,2\pi] \rightarrow \mathbb{R}, tal que f(x)= 2x+sen \, x\; cumple las hipótesis del teorema de Lagrange, y determina los puntos a los que hace referencia dicho teorema.

[editar]

Ejercicios

Problema (4'18")     Sinopsis:

Si el lado de un cuadrado aumenta a una velocidad constante de 3cm/seg, halla la velocidad a la que aumenta el área del cudrado cuando el lado mide 12 cm, y calcula el valor del lado cuando el área crece a 60 cm2/seg.

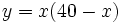
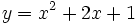
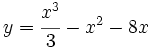Obtenido de "http://maralboran.org/wikipedia/index.php/Aplicaciones_de_la_derivada_%282%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda