Plantilla:Relación entre ángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:30 4 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:51 4 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
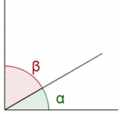
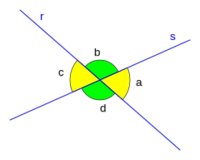
| - | {{Tabla75|celda2=<center>[[Imagen:angulos_consec.png|200px]]{{p}}Ángulos consecutivos.</center> | + | {{Tabla75|celda2={{p}}[[Imagen:angulos_consec.png|200px|center]]<br><center>Ángulos consecutivos</center><br>{{p}}<br>[[Imagen:angulos_opuestos_vertice.png|200px|center]]<center>'''a''' y '''c''' son opuestos por el vértice,{{p}}al igual que '''b''' y '''d'''</center> |
| |celda1= | |celda1= | ||
| {{Caja_Amarilla|texto=*Dos ángulos son '''iguales''' si tienen la misma amplitud. | {{Caja_Amarilla|texto=*Dos ángulos son '''iguales''' si tienen la misma amplitud. | ||
| - | *Dos ángulos son '''consecutivos''' si tienen el vértice y un lado en común.}} | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Caja_Amarilla|texto= | ||
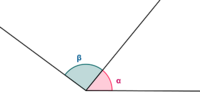
| * Ángulos '''complementarios '''son aquellos cuya suma es un ángulo recto. | * Ángulos '''complementarios '''son aquellos cuya suma es un ángulo recto. | ||
| - | {{p}} | ||
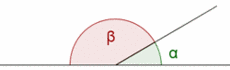
| * Ángulos '''suplementarios '''son aquellos cuya suma es un ángulo llano. | * Ángulos '''suplementarios '''son aquellos cuya suma es un ángulo llano. | ||
| + | *Dos ángulos son '''consecutivos''' si tienen el vértice y un lado en común. | ||
| + | *Dos ángulos son '''adyacentes''' si tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. Por tanto son consecutivos y suplementarios simultáneamente. | ||
| + | * Ángulos '''opuestos por el vértice '''son aquellos que cumplen que los lados de uno son semirrectas opuestas a los lados del otro. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | <br> | ||
| {{Tabla50|celda1=[[Imagen:angulos_complementarios.gif|120px|center]]{{p}}<center>Ángulos complementarios</center> | {{Tabla50|celda1=[[Imagen:angulos_complementarios.gif|120px|center]]{{p}}<center>Ángulos complementarios</center> | ||
| - | |celda2=<br><br>[[Imagen:angulos_suplementarios.gif|230px|center]]{{p}}<center>Ángulos complementarios</center>}} | + | |celda2=<br><br>[[Imagen:angulos_suplementarios.gif|230px|center]]{{p}}<center>Ángulos suplementarios</center> |
| + | }} | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| Línea 20: | Línea 21: | ||
| |sinopsis=Ángulos complementarios y suplementarios. Ejemplos. | |sinopsis=Ángulos complementarios y suplementarios. Ejemplos. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Tabla75|celda2=[[Imagen:angulos_opuestos_vertice.png|200px|center]] | ||
| - | |celda1= | ||
| - | {{Caja_Amarilla|texto= | ||
| - | * Ángulos '''opuestos por el vértice '''son aquellos que cumplen que los lados de uno son semirrectas opuestas a los lados del otro. | ||
| - | }} | ||
| - | {{p}} | ||
| - | En la imagen de la derecha, '''a''' y '''c''' son opuestos por el vértice, al igual que '''b''' y '''d'''. | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| Línea 37: | Línea 30: | ||
| |descripcion=Actividad en la que podrás observar las distintas relaciones que hay entre ángulos. | |descripcion=Actividad en la que podrás observar las distintas relaciones que hay entre ángulos. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_3c.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_3c.htm | ||
| - | }} | ||
| }} | }} | ||
Revisión de 16:51 4 jul 2017
|  Ángulos consecutivos
 |
Ángulos complementarios y suplementarios (9´19") Sinopsis:Ángulos complementarios y suplementarios. Ejemplos.
En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice.
Relaciones entre ángulos Descripción: Actividad en la que podrás observar las distintas relaciones que hay entre ángulos.
