Ángulos en la circunferencia (1º ESO)
De Wikipedia
| Revisión de 10:24 6 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:30 6 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| {{Ángulo inscrito}} | {{Ángulo inscrito}} | ||
| - | ==Otros ángulos== | + | ==Actividades y videotutoriales== |
| - | {{otros ángulos}} | + | |
| - | + | ||
| - | ==Actividades== | + | |
| {{AI_anaya | {{AI_anaya | ||
| |titulo1=Actividad: ''Ángulos en la circunferencia'' | |titulo1=Actividad: ''Ángulos en la circunferencia'' | ||
| Línea 28: | Línea 25: | ||
| |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/05.htm | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/05.htm | ||
| }} | }} | ||
| + | {{otros ángulos}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 12:30 6 jul 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
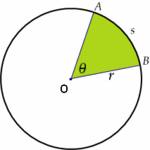
Ángulo central
En esta actividad podrás ver cómo es un ángulo central y el arco de circunferencia que determina.
Ángulo inscrito
Propiedades
Propiedades
- Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
- La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- Todo ángulo inscrito en una semicircunferencia es recto.
Las dos primeras propiedades se pueden comprobar (no es una demostración) en la siguiente escena:
En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
La tercera propiedad la puedes comprobar en esta otra escena:
En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia.
En esta actividad podrás ver cómo es un ángulo inscrito y su relación con el ángulo central correspondiente.
En esta actividad podrás ver cómo un ángulo inscrito en una semicircunferencia es recto.
Actividades y videotutoriales
Ángulos en una circunferencia: Interior, central, inscrito, semiinscrito, interior y circunscrito.
En esta escena podrás ver los distintos tipos de ángulos que puede haber en una circunferencia: central, inscrito, semiinscrito, circunscrito, interior, exterior.
En esta escena podrás practicar el cálculo del valor de distintos tipos de ángulos en una circunferencia.
 y su arco correspondiente AB.
y su arco correspondiente AB.
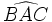 .
.