Plantilla:Representación de fracciones en la recta numérica
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:10 7 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:16 7 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Representación de fracciones en la recta numérica | ||
| + | |descripcion=Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_contenidos_1c.htm | ||
| + | }} | ||
| + | {{}} | ||
| {{Videotutoriales|titulo=Representación gráfica de las fracciones|enunciado= | {{Videotutoriales|titulo=Representación gráfica de las fracciones|enunciado= | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
Revisión de 08:16 7 jul 2017
Procedimiento
- Para ubicar una fracción propia en la recta numérica se divide el segmento unidad en partes iguales, como indica el denominador, y se ubica la facción según indica el numerador.
- Si la fracción es impropia se pasa a forma mixta ("valor entero" + "fracción propia") y se representa las "fracción propia" en la siguiente unidad al "valor entero" obtenido.
Ejemplo: Representación de fracciones en la recta numérica
Representa las fracciones:
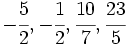
Solución:
Nota: Pasa las fracciones impropias a forma mixta.
Representación de fracciones en la recta numérica Descripción: Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica.
{{}}
Tutorial 1 (19'26") Sinopsis:Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Tutorial 2 (12'44") Sinopsis: Representación del conjunto de los racionales en la recta real.
Representación de fracciones en la recta numérica Descripción: En esta escena podrás comprobar si sabes representar fracciones en la recta numérica.
Actividad: Representación de fracciones en la recta numérica
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
