Plantilla:Periodicidad de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:28 15 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 3: | Línea 3: | ||
| {{Caja Amarilla | {{Caja Amarilla | ||
| |texto= | |texto= | ||
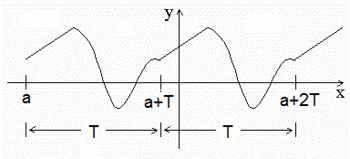
| - | Una función es '''periódica''' si su gráfica se va repitiendo cada cierto valor de la variable independiente <math>x</math>. A dicho valor se le llama '''periodo'''. | + | Una función es '''periódica''' si su gráfica se va repitiendo a intervalos. Al menor valor posible, T, de la longitud de dicho intervalo, se le llama '''periodo'''. |
| Se cumple:{{p}} | Se cumple:{{p}} | ||
| - | <center><math>f(x)=f(x+p),\quad \forall x \in D_f \quad (p=periodo)</math></center> | + | <center><math>f(x)=f(x+T),\quad \forall x \in Dom_f</math></center> |
| }} | }} | ||
| |celda2=<center>[[Imagen:periodica.gif |350px|Función de periodo p]]</center> | |celda2=<center>[[Imagen:periodica.gif |350px|Función de periodo p]]</center> | ||
| - | }}{{p}} | + | }} |
| - | {{AI2|titulo=Actividad interactiva: ''Periodicidad'' | + | {{p}} |
| + | {{AI_cidead | ||
| + | |titulo1=Periodicidad de una función | ||
| + | |descripcion=Actividades con las que aprenderás a determinar si una función es periódica y a hallar su período a partir de su gráfica. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena9/3quincena9_contenidos_2f.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Funciones periódicas|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Funciones periódicas'' | ||
| |cuerpo= | |cuerpo= | ||
| - | {{ai_cuerpo | + | {{ejercicio_cuerpo |
| - | |enunciado=1. Autoevaluación. | + | |enunciado= |
| - | |actividad= | + | |
| - | <center><iframe> | + | :En próximos cursos estudiarás las funciones trigonométricas, como las funciones seno o coseno. A continuación podrás ver su aspecto y su período: |
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayerP3V?p3v=true&xref=200412031130_AC_0_1491598710&mode=1&rtc=1001&locale=es&cache=false',750,540,'snrPop',0 | + | |
| - | width=100% | + | :a) Período de la función seno. |
| - | height=700 | + | :b) Período de la función coseno. |
| - | name=myframe | + | |
| - | </iframe></center> | + | {{p}} |
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=period sin(x)}} | ||
| + | :b) {{consulta|texto=period cos(x)}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_estudiia | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=3'41" | ||
| + | |url1=https://www.youtube.com/watch?v=dTgrxlz6bMs | ||
| + | |sinopsis=Estudio de la periodicidad de una función dada por una gráfica. | ||
| }} | }} | ||
Revisión actual
Una función es periódica si su gráfica se va repitiendo a intervalos. Al menor valor posible, T, de la longitud de dicho intervalo, se le llama periodo. Se cumple: |  |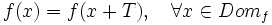
Periodicidad de una función Descripción: Actividades con las que aprenderás a determinar si una función es periódica y a hallar su período a partir de su gráfica.
Actividad: Funciones periódicas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio (3'41") Sinopsis:Estudio de la periodicidad de una función dada por una gráfica.
