Plantilla:Máximos y mínimos de una función
De Wikipedia
| Revisión de 08:35 12 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:05 12 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Máximos y mínimos|enunciado= | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Máximos y mínimos | + | |titulo1=Tutorial |
| |duracion=8'08" | |duracion=8'08" | ||
| |url1=https://www.youtube.com/watch?v=6j-5Gw2K-9E&index=11&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | |url1=https://www.youtube.com/watch?v=6j-5Gw2K-9E&index=11&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| |sinopsis=Tutorial en el que se explica el estudio de Máximos y Mínimos (relativos y absolutos) de una función dada su gráfica. | |sinopsis=Tutorial en el que se explica el estudio de Máximos y Mínimos (relativos y absolutos) de una función dada su gráfica. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=1'11" | ||
| + | |url1=https://www.youtube.com/watch?v=4NqRxo22Yco&list=PLC972B19E61810C49&index=2 | ||
| + | |sinopsis=Estudio de los puntos extremos de una función a partir de su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=1'10" | ||
| + | |url1=https://www.youtube.com/watch?v=4TxciFxQO58&list=PLC972B19E61810C49&index=3 | ||
| + | |sinopsis=Estudio de los puntos extremos de una función a partir de su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=1'29" | ||
| + | |url1=https://www.youtube.com/watch?v=dhhKSWuU0SM&list=PLC972B19E61810C49&index=4 | ||
| + | |sinopsis=Estudio de los puntos extremos de una función a partir de su gráfica. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:05 12 jul 2017
- Una función
 tiene un máximo relativo en un punto
tiene un máximo relativo en un punto 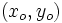 cuando
cuando 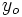 es mayor que los valores que toma la variable
es mayor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
- Una función
 tiene un mínimo relativo en un punto
tiene un mínimo relativo en un punto 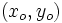 cuando
cuando 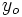 es menor que los valores que toma la variable
es menor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
Actividades con las que aprenderás a determinar los máximos y mínimos de una función dada gráficamente.
Tutorial en el que se explica el estudio de Máximos y Mínimos (relativos y absolutos) de una función dada su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
En esta escena podrás ver cuando una función alcanza un máximo o un mínimo.
Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. Averigua sus máximos y mínimos relativos.
Construye una gráfica que cumpla ciertas condiciones sobre los puntos por los que pasa. Se exigira, por ejemplo, que tenga máximos o mínimos en ciertos puntos, que tenga ciertos puntos de corte con los ejes, etc.

