Plantilla:Posición circ-circ
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:22 22 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:23 22 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| *'''Coincidentes''', si tienen el mismo centro y el mismo radio. | *'''Coincidentes''', si tienen el mismo centro y el mismo radio. | ||
| :En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes. | :En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| <center>[[Imagen:dosCircunferencias.jpg]]</center> | <center>[[Imagen:dosCircunferencias.jpg]]</center> | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
Revisión de 09:23 22 jul 2017
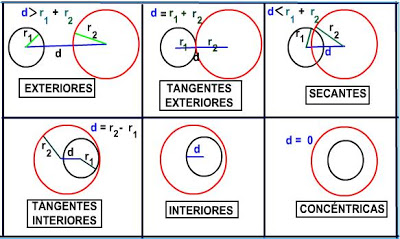
Dos circunferencias pueden ser:
- Exteriores, si no tienen puntos comunes.
- Cumplen que la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio.
- Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. :Cumplen que la distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio.
- Secantes, si se cortan en dos puntos distintos.
- Cumplen que la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos.
- Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto.
- Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente.
- Cumplen que la distancia que hay entre sus centros es igual a la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores excéntricas, si no tienen ningún punto común.
- Cumplen que la distancia entre sus centros es mayor que 0 y menor que la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores concéntricas, si tienen el mismo centro y distinto radio.
- Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra.
- Coincidentes, si tienen el mismo centro y el mismo radio.
- En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes.
