Rectángulo cordobés (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 23:50 23 jul 2017 Coordinador (Discusión | contribuciones) (→El triángulo cordobés) ← Ir a diferencia anterior |
Revisión de 23:56 23 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| ==El rectángulo cordobés== | ==El rectángulo cordobés== | ||
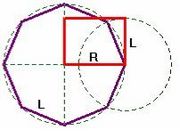
| - | {{Tabla75|celda2=[[Imagen:rec_cordobes.jpg|center|thumb|Rectángulo cordobés en color rojo.]]|celda1= | + | {{Tabla75|celda2=[[Imagen:rec_cordobes.jpg|center|thumb|Rectángulo cordobés, en color rojo.]]|celda1= |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *El '''rectángulo cordobés''' es un rectángulo que muestra una proporción entre sus lados, R y L, igual a | *El '''rectángulo cordobés''' es un rectángulo que muestra una proporción entre sus lados, R y L, igual a | ||
| Línea 40: | Línea 40: | ||
| ==El triángulo cordobés== | ==El triángulo cordobés== | ||
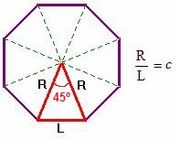
| - | {{Tabla75|celda2=[[Imagen:tri_cordobes.jpg|center|thumb|Triángulo cordobés en color rojo.]]|celda1= | + | {{Tabla75|celda2=[[Imagen:tri_cordobes.jpg|center|thumb|Triángulo cordobés, en color rojo.]]|celda1= |
| {{Caja_Amarilla|texto=El '''triángulo cordobés''' es un triángulo isósceles cuyos lados iguales, de medida R, y su lado desigual, de medida L, están en proporción cordobesa | {{Caja_Amarilla|texto=El '''triángulo cordobés''' es un triángulo isósceles cuyos lados iguales, de medida R, y su lado desigual, de medida L, están en proporción cordobesa | ||
Revisión de 23:56 23 jul 2017
El rectángulo cordobés
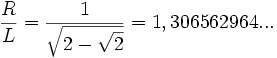
Su descubrimiento y estudio se debe al arquitecto afincado en Córdoba, Rafael de la Hoz Arderius (1924-2000), el cual, en el estudio de las razones en las dimensiones de la Mezquita de Córdoba y otros diseños árabes de la urbe andaluza, se encontró reiteradas veces con dicho número. |  |
El triángulo cordobés
El triángulo cordobés es un triángulo isósceles cuyos lados iguales, de medida R, y su lado desigual, de medida L, están en proporción cordobesa |  |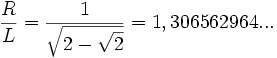
