Números complejos: Operaciones (1ºBach)
De Wikipedia
| Revisión de 11:14 26 jul 2017 Coordinador (Discusión | contribuciones) (→Operaciones con números complejos en forma binómica) ← Ir a diferencia anterior |
Revisión de 11:15 26 jul 2017 Coordinador (Discusión | contribuciones) (→Operaciones con números complejos en forma binómica) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| *Propiedades. | *Propiedades. | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1= Producto de números complejos | |titulo1= Producto de números complejos | ||
| Línea 40: | Línea 39: | ||
| *Propiedades. | *Propiedades. | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1= Cociente de números complejos | |titulo1= Cociente de números complejos | ||
| Línea 49: | Línea 47: | ||
| *Ejemplos. | *Ejemplos. | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1= Potenciación de números complejos expresados en forma binómica | |titulo1= Potenciación de números complejos expresados en forma binómica | ||
| Línea 56: | Línea 53: | ||
| |sinopsis=Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en [[Números complejos: Operaciones en forma polar (1ºBach)#Potencias de números complejos en forma polar|forma polar]] como se verá en otro apartado de este tema. | |sinopsis=Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en [[Números complejos: Operaciones en forma polar (1ºBach)#Potencias de números complejos en forma polar|forma polar]] como se verá en otro apartado de este tema. | ||
| }} | }} | ||
| - | --- | + | ---- |
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| |titulo1=Ejemplos | |titulo1=Ejemplos | ||
Revisión de 11:15 26 jul 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 150)
Operaciones con números complejos en forma binómica
- Suma:
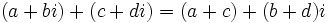
- Resta:
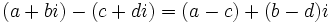
- Multiplicación:
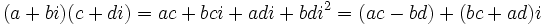
- División:
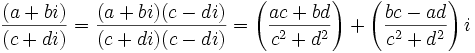 , siempre que
, siempre que 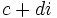 no sea nulo.
no sea nulo.
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
- Definición de producto de números complejos en forma binómica.
- Ejemplos.
- Propiedades.
- Definición de cociente de números complejos en forma binómica.
- Ejemplos.
Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en forma polar como se verá en otro apartado de este tema.
Ejemplos de suma, resta, multiplicación y división de números complejos en forma binómica.
Ejemplos: Operaciones con complejos en forma binómica
Efectúa las siguientes operaciones:
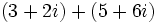
Solución:
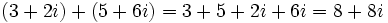
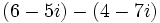
Solución:
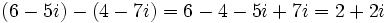

Solución:
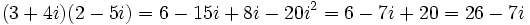
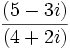
Solución:
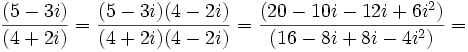
Dados los complejos 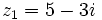 y
y 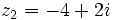 , halla:
, halla:
a) 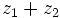
b) 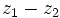 .
.
Dados los complejos 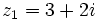 y
y 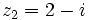 , halla:
, halla:
a) 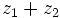
b) 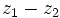 .
.
Dados los complejos 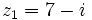 y
y 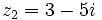 , halla:
, halla:
a) 
b)  .
.
Dados los complejos 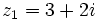 y
y 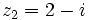 , halla:
, halla:
a) 
b)  .
.
Dados los complejos 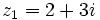 y
y 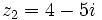 , halla:
, halla:
a) 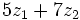
b) 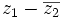
c) 
d) 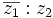
e) 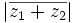
Dados los complejos 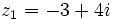 y
y 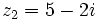 , halla:
, halla:
a) 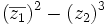
b)  .
.
Operaciones en forma binómica.
Operaciones en forma binómica.
Operaciones en forma binómica.
Potencias en forma binómica.
Operaciones en forma binómica.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Representación gráfica de las operaciones con complejos en forma binómica
En esta escena podrás ver como se representa la suma de números complejos en forma binómica.
En esta escena podrás ver como se representa la resta de números complejos en forma binómica.
En esta escena podrás ver como se representa la multiplicación de números complejos en forma binómica.
En esta escena podrás ver como se representa la división de números complejos en forma binómica.
(Pág. 151)
Propiedades de las operaciones con números complejos
Propiedades
- Propiedades de la suma:
- Asociativa:
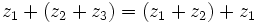
- Conmutativa:
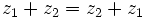
- Existencia de elemento neutro: El 0 es el elemento neutro de la suma.
- Existencia de opuesto: Todo número complejo,
 , tiene un opuesto,
, tiene un opuesto, 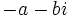
- Asociativa:
- Propiedades del producto:
- Asociativa:
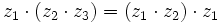
- Conmutativa:
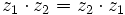
- Existencia de elemento neutro: El 1 es el elemento neutro del producto.
- Existencia de inverso: Todo número complejo,
 , distinto de 0, tiene inverso,
, distinto de 0, tiene inverso, 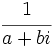 :
:
- Asociativa:
- Propiedad distributiva del producto respecto de la suma:
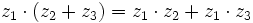
Ejercicios
Ejercicios resueltos
a) Obtener un polinomio de segundo grado cuyas raíces sean 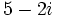 y
y 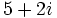 .
.
b) ¿Cuánto ha de valer x para que 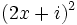 sea imaginario puro?
sea imaginario puro?
a) ![P(x)= [x-(5-2i)][x-(5+2i)]= \cdots = x^2-10x+29\;](/wikipedia/images/math/8/8/e/88e9c5ab01582d012973933375683cfa.png)
b) Hay que desarrollar el cuadrado e igualar la parte real a cero.
Solución: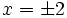
Dados los complejos 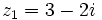 ,
, 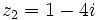 ,
, 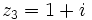 y
y 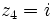 , calcula:
, calcula:
a) 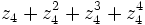 .
.
b) 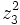
c) 
d) 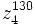
e) 
f) 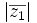
Dados los complejos 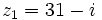 y
y 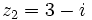 , halla el módulo de
, halla el módulo de 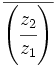 .
.
Calcula: 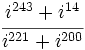 .
.
a) Halla el valor de "x" sabiendo que 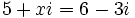 .
.
b) Sea 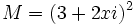 .¿Qué valor debe tomar "x" para que M sea imaginario puro? ¿Y para que M sea un número real?
.¿Qué valor debe tomar "x" para que M sea imaginario puro? ¿Y para que M sea un número real?
Calcula "m" y "n" para que sea cierta la igualdad 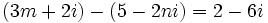 .
.
Halla dos números complejos cuyo cociente sea imaginario puro, su suma sea 5 y el módulo del dividendo sea doble del módulo del divisor.
Calcula el valor de "x" de manera que 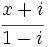 sea:
sea:
a) Igual a 1+2i.
b) Un número real.
c)Un número imaginario puro.
Dados los dos números complejos, 2-mi y 3-ni, halla los valores de "m" y "n" de manera que el producto de los complejos dados sea 8-4i.
Ejercicios varios.
|
Actividad: Operaciones con complejos a) Halla un polinomio de segundo grado cuyas raíces sean b) Halla x para que c) Halla la parte imaginaria de Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) expand [x-(2+i)][x-(2-i)] b) solve Re[(2+x*i)^2]=0 c) Im[(1-i)^3] |
Ejercicios propuestos
|
Ejercicios propuestos: Operaciones con números complejos |
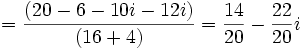
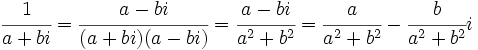
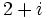 y
y 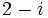 .
.
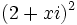 sea imaginario puro.
sea imaginario puro.