Plantilla:Continuidad de funciones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:05 11 oct 2014 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{caja Amarilla | {{caja Amarilla | ||
| |texto= | |texto= | ||
| - | Cuando la gráfica de una función tiene saltos bruscos (no se puede dibujar de un solo trazo) decimos que es '''discontinua'''. En caso contrario se dice que es '''continua'''. Los puntos donde se producen los saltos se llaman '''discontinuidades'''. | + | *Cuando la gráfica de una función tiene saltos bruscos (no se puede dibujar de un solo trazo) decimos que es '''discontinua'''. En caso contrario se dice que es '''continua'''. Los puntos donde se producen los saltos se llaman '''discontinuidades'''. |
| + | *Una función diremos que es '''continua en un intervalo''' si no presenta ninguna discontinuidad en dicho intervalo, aunque pueda presentar alguna fuera del mismo. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejercicio | + | {{Ejemplo|titulo=Ejemplos: ''Continuidad''|enunciado=De las siguientes funciones, indica cuáles son continuas y cuáles no. Enumera las discontinuidades. |
| - | |titulo=Ejercicios: ''Continuidad'' | + | {{p}} |
| - | |cuerpo= | + | :a)[[Imagen:funcion1d.png]]{{b}}b)[[Imagen:funcion1e.png]] c)[[Imagen:funcion1f.png]] |
| + | {{p}} | ||
| + | |sol= | ||
| + | '''Solución:''' | ||
| - | {{ejercicio_cuerpo | + | Las funciones a) y c) son continuas. |
| - | |enunciado= | + | |
| - | '''1. '''De las siguientes funciones, indica cuáles son continuas y cuáles no. Enumera las discontinuidades.<br> | + | La b) es discontinua con discontinuidades en <math>x=-1\;</math> y <math>x=3\;</math>. |
| - | a)[[Imagen:funcion1d.png]]{{b}}b)[[Imagen:funcion1e.png]] c)[[Imagen:funcion1f.png]] | + | }} |
| {{p}} | {{p}} | ||
| - | |sol= | + | {{AI_cidead |
| - | Las funciones a) y c) son continuas. La b) es discontinua con discontinuidades en <math>x=-1</math> y <math>x=3</math>. | + | |titulo1=Continuidad de funciones |
| + | |descripcion=Actividades en las que aprenderás el concepto de continuidad de una función. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena9/3quincena9_contenidos_2b.htm | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Continuidad de funciones|enunciado= | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=9´19" | ||
| + | |url1=https://www.youtube.com/watch?v=SCcMFf4gAks | ||
| + | |sinopsis=Concepto de función continua y de función continua en un intervalo. Ejemplos. | ||
| }} | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=5'36" | ||
| + | |url1=https://www.youtube.com/watch?v=R8h56wRKZM4&index=8&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| + | |sinopsis=Tutorial en el que se explica el estudio de la continuidad de una función dada su gráfica, así como los tipos de discontinuidades que existen. | ||
| {{p}} | {{p}} | ||
| + | '''Nota 1:''' En este tutorial se definen algunos "tipos de discontinuidades" que nosotros no veremos hasta proximos cursos. No obstante, son bastante intuitivos y se podrán entender sin mayor problema. | ||
| + | |||
| + | '''Nota 2:''' A lo largo del tutorial se ve un ejemplo en el que la función no está definida en un intervalo y se dice que la función es discontinua en todo ese intervalo. En cursos superiores, diremos que en esos intervalos donde la función no está definida "no tiene sentido" hablar de continuidad ni de discontinuidad. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=1'33" | ||
| + | |url1=https://www.youtube.com/watch?v=SeyibueKLkk&index=1&list=PL70484B1A25A15C5B | ||
| + | |sinopsis=Estudio de la continuidad de una función a partir de su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=0'56" | ||
| + | |url1=https://www.youtube.com/watch?v=eIJWASeObmA&index=2&list=PL70484B1A25A15C5B | ||
| + | |sinopsis=Estudio de la continuidad de una función a partir de su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=0'49" | ||
| + | |url1=https://www.youtube.com/watch?v=ZTiCyB35mYc&index=3&list=PL70484B1A25A15C5B | ||
| + | |sinopsis=Estudio de la continuidad de una función a partir de su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=1'04" | ||
| + | |url1=https://www.youtube.com/watch?v=jVHCyCUfJGk&index=4&list=PL70484B1A25A15C5B | ||
| + | |sinopsis=Estudio de la continuidad de una función a partir de su gráfica. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Continuidad de funciones|contenido= | ||
| {{wolfram | {{wolfram | ||
| |titulo=Actividad: ''Continuidad de funciones'' | |titulo=Actividad: ''Continuidad de funciones'' | ||
| Línea 25: | Línea 74: | ||
| |enunciado= | |enunciado= | ||
| - | Observa las gráficas de las siguientes funciones y si tiene o no discontinuidades: | + | Observa las gráficas de las siguientes funciones y si tienen o no discontinuidades: |
| :a) <math>y=x^3+x\;</math> no presenta discontinuidades. | :a) <math>y=x^3+x\;</math> no presenta discontinuidades. | ||
| :b) <math>y=\frac{1}{x}</math> presenta una discontinuidad en x=0. | :b) <math>y=\frac{1}{x}</math> presenta una discontinuidad en x=0. | ||
| - | + | :b) <math>y=\frac{1}{x}\, , \ x \in [1,10]</math> no presenta discontinuidades en ese intervalo. | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) Obtén el dominio y la imagen de la función <math>y=x^3+x</math>. | + | |
| - | :b) Obtén el dominio y la imagen de la función <math>y=\frac{1}{x}</math>. | + | |
| - | + | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| Línea 42: | Línea 84: | ||
| :a) {{consulta|texto=plot x^3+x}} | :a) {{consulta|texto=plot x^3+x}} | ||
| - | :b) {{consulta|texto=plot 1/x}} | + | :b) {{consulta|texto= plot 1/x}} |
| + | :c) {{consulta|texto= plot 1/x, x from 1 to 10}} | ||
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| - | + | }} | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
- Cuando la gráfica de una función tiene saltos bruscos (no se puede dibujar de un solo trazo) decimos que es discontinua. En caso contrario se dice que es continua. Los puntos donde se producen los saltos se llaman discontinuidades.
- Una función diremos que es continua en un intervalo si no presenta ninguna discontinuidad en dicho intervalo, aunque pueda presentar alguna fuera del mismo.
Ejemplos: Continuidad
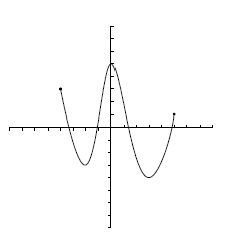
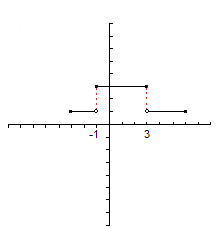
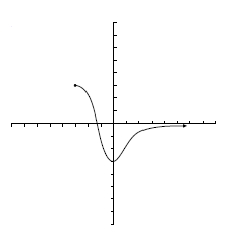
De las siguientes funciones, indica cuáles son continuas y cuáles no. Enumera las discontinuidades.
- a)
b)
c)
Solución:
Solución:
Las funciones a) y c) son continuas.
La b) es discontinua con discontinuidades en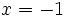
y 
.
Continuidad de funciones Descripción: Actividades en las que aprenderás el concepto de continuidad de una función.
Tutorial 1 (9´19") Sinopsis:Concepto de función continua y de función continua en un intervalo. Ejemplos.
Tutorial 2 (5'36") Sinopsis:Tutorial en el que se explica el estudio de la continuidad de una función dada su gráfica, así como los tipos de discontinuidades que existen.
Nota 1: En este tutorial se definen algunos "tipos de discontinuidades" que nosotros no veremos hasta proximos cursos. No obstante, son bastante intuitivos y se podrán entender sin mayor problema.
Nota 2: A lo largo del tutorial se ve un ejemplo en el que la función no está definida en un intervalo y se dice que la función es discontinua en todo ese intervalo. En cursos superiores, diremos que en esos intervalos donde la función no está definida "no tiene sentido" hablar de continuidad ni de discontinuidad.
Ejercicio 1 (1'33") Sinopsis:Estudio de la continuidad de una función a partir de su gráfica.
Ejercicio 2 (0'56") Sinopsis:Estudio de la continuidad de una función a partir de su gráfica.
Ejercicio 3 (0'49") Sinopsis:Estudio de la continuidad de una función a partir de su gráfica.
Ejercicio 4 (1'04") Sinopsis:Estudio de la continuidad de una función a partir de su gráfica.
Actividad: Continuidad de funciones Observa las gráficas de las siguientes funciones y si tienen o no discontinuidades:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
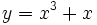no presenta discontinuidades.
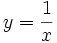presenta una discontinuidad en x=0.
![y=\frac{1}{x}\, , \ x \in [1,10]](/wikipedia/images/math/b/d/6/bd68b28d4862afc025e586193eac9bf1.png)
no presenta discontinuidades en ese intervalo.
