Plantilla:Area trapecio
De Wikipedia
| Revisión de 10:22 29 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:45 29 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 23: | Línea 23: | ||
| |url1=https://www.youtube.com/watch?v=Of2t3zcNtuM | |url1=https://www.youtube.com/watch?v=Of2t3zcNtuM | ||
| |sinopsis=El trapecio y su área. Ejemplo.}} | |sinopsis=El trapecio y su área. Ejemplo.}} | ||
| - | {{Video_enlace | + | {{Video_enlace_velazco |
| |titulo1=Área del trapecio (demostración) | |titulo1=Área del trapecio (demostración) | ||
| |duracion=4´27" | |duracion=4´27" | ||
Revisión de 10:45 29 jul 2017
El trapecio y su área. Ejemplo.
Demostración de la fórmula del área de un trapecio.
Halla el área de un trapecio isósceles que tiene 8 cm de base menor, 12 cm de base mayor y 5 cm de lados no paralelos.
Halla el área y el perímetro de un trapecio isósceles que tiene 9 cm de base menor, 15 cm de base mayor y 5 cm de lados no paralelos.
Halla el área de un trapecio isósceles que tiene 9 cm de base menor, 12 cm de base mayor y 5 cm de lados no paralelos.
Esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del trapecio; en la segunda podrás aplicar dicha fórmula en un caso práctico.
En esta escena podrás deducir la fórmula del área del trapecio de otra manera. Además podrás realizar el cálculo del área en una actividad.
Ejercicio resuelto: Área del trapecio
Halla el área de un trapecio isósceles cuyas bases miden 37 cm y 55 cm, y el lado oblicuo, 14 cm.
Utilizando el teorema de Pitágoras se halla la altura a=10.7 cm. A continuación se aplica la fórmula para hallar el área.
Solución: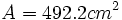
|
Actividad: El trapecio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
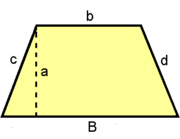
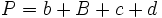
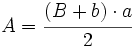
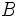 : base mayor.
: base mayor.
 : base menor.
: base menor.
 : altura.
: altura.
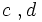 : lados.
: lados.

