Ejercicios: Cálculo de primitivas (2ºBach)

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 19:31 29 jul 2017

Ejercicio 1 (1'53") Sinopsis:

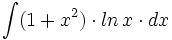
$\int (1+x^2) \cdot ln \, x \cdot dx$

Ejercicio 2 (3'20") Sinopsis:

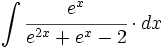
$\int \cfrac{e^x}{e^{2x}+e^x-2} \cdot dx$

Ejercicio 3 (3'20") Sinopsis:

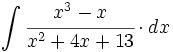
$\int \cfrac{x^3-x}{x^2+4x+13} \cdot dx$

Ejercicio 4 (3'05") Sinopsis:

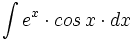
$\int e^x \cdot cos \, x \cdot dx$

Ejercicio 5 (3'26") Sinopsis:

$\int \cfrac{1}{\sqrt[3]{x^2} \cdot (\sqrt[3]{x^2}+\sqrt[3]{x}+1)} \cdot dx$

Ejercicio 6 (2'55") Sinopsis:

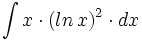
$\int x \cdot (ln \, x)^2 \cdot dx$

Ejercicio 7 (1'30") Sinopsis:

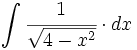
$\int \cfrac{1}{\sqrt{4-x^2}} \cdot dx$

Ejercicio 8 (6'04") Sinopsis:

$\int \cfrac{x^2+3x+2}{(x-1)(x^2+2x+2)} \cdot dx$

Ejercicio 9 (1'44") Sinopsis:

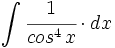$\int \cfrac{1}{cos^4 \, x} \cdot dx$ mediante cambio de variable $tg \, x = z$ .

Ejercicio 10 (3'41") Sinopsis:

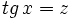Hallar 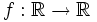$f: \mathbb{R} \rightarrow \mathbb{R}$ tal que f(0)=0, f'(=)=5, f(0)=1 y f'(x)=x+1

Ejercicio 11 (3'41") Sinopsis:

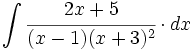
$\int \cfrac{2x+5}{(x-1)(x+3)^2} \cdot dx$

Ejercicio 12 (3'03") Sinopsis:

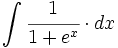
$\int \cfrac{1}{1+e^x} \cdot dx$

Ejercicio 13 (2'06") Sinopsis:

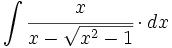
$\int \cfrac{x}{x-\sqrt{x^2-1}} \cdot dx$

Ejercicio 14 (1'55") Sinopsis:

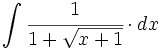
$\int \cfrac{1}{1+\sqrt{x+1}} \cdot dx$

Ejercicio 15 (3'04") Sinopsis:

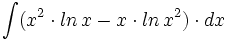
$\int (x^2 \cdot ln \, x -x \cdot ln \, x^2) \cdot dx$

Ejercicio 16 (2'48") Sinopsis:

Halla una primitiva de 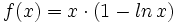$f(x)=x \cdot (1-ln \, x)\;$ que pase por el punto (1,1).

Ejercicio 17 (5'00") Sinopsis:

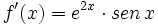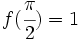Determina f(x) sabiendo que $f'(x)=e^{2x} \cdot sen \, x\;$ y que $f(\cfrac{\pi}{2})=1$ .

Ejercicio 18 (6'05") Sinopsis:

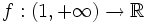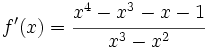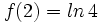Determina $f:(1, +\infty)\rightarrow \mathbb{R}$ sabiendo que $f'(x)=\cfrac{x^4-x^3-x-1}{x^3-x^2}$ y que $f(2)=ln \, 4$ .

Ejercicio 19 (1'57") Sinopsis:

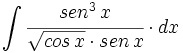
$\int \cfrac{sen^3 \, x}{\sqrt{cos \, x} \cdot sen \, x} \cdot dx$

Ejercicio 20 (1'33") Sinopsis:

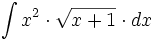
$\int x^2 \cdot \sqrt{x+1} \cdot dx$

Ejercicio 21 (1'33") Sinopsis:

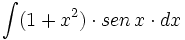
$\int (1+x^2) \cdot sen \, x \cdot dx$

Ejercicio 22 (1'15") Sinopsis:

Calcula una función que valga cero en el punto x=0 y cuya derivada sea f(x)=sen \, x \cdot cos \, x.

Ejercicio 23 (4'36") Sinopsis:

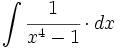
$\int \cfrac{1}{x^4-1} \cdot dx$

Ejercicio 24 (2'08") Sinopsis:

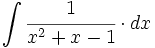
$\int \cfrac{1}{x^2+x-1} \cdot dx$

Ejercicio 25 (2'56") Sinopsis:

Determina las funciones cuya segunda derivada es f(x)=x \cdot e^x, y obtener la que pasa por los puntos (0,2) y (2,0).

Ejercicio 26 (3'20") Sinopsis:

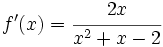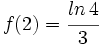Halla f(x) sabiendo que $f'(x)=\cfrac{2x}{x^2+x-2}$ y que $f(2)=\cfrac{ln \, 4}{3}$ .

Ejercicio 27 (1'10") Sinopsis:

$\int \cfrac{\sqrt{5x^3}+\sqrt[3]{3x^2}}{\sqrt{2x}} \cdot dx$

Ejercicio 28 (1'12") Sinopsis:

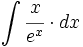
$\int \cfrac{x}{e^x} \cdot dx$

Ejercicio 29 (3'06") Sinopsis:

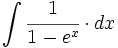
$\int \cfrac{1}{1-e^x} \cdot dx$

Ejercicio 30 (3'05") Sinopsis:

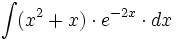
$\int (x^2+x) \cdot e^{-2x} \cdot dx$

Ejercicio 31 (3'24") Sinopsis:

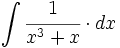
$\int \cfrac{1}{x^3+x} \cdot dx$

Ejercicio 32 (2'22") Sinopsis:

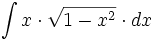
$\int x \cdot \sqrt{1-x^2} \cdot dx$

Ejercicio 33 (1'40") Sinopsis:

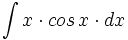
$\int x \cdot cos \, x \cdot dx$

Integrales trigonométricas Descripción:

Una completa colección de videos sobre integrales trigonométricas.

Obtenido de "http://maralboran.org/wikipedia/index.php/Ejercicios:_C%C3%A1lculo_de_primitivas_%282%C2%BABach%29"

Vistas

Herramientas personales

Registrarse/Entrar

Menú

Buscar

Herramientas

* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda