Plantilla:Sucesos
De Wikipedia
| Revisión de 09:48 15 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Operaciones con sucesos. Sucesos compatibles e incompatibles) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *'''Suceso''' de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral {{sube|porcentaje=+20%|contenido=<math> | + | *Llamaremos '''suceso''' de un experimento aleatorio a cada uno de los subconjuntos del espacio muestral {{sube|porcentaje=+20%|contenido=<math> |
| E\, | E\, | ||
| - | </math>}}. Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas. | + | </math>}}. Para designar cualquier suceso utilizaremos letras mayúsculas. |
| *Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama '''espacio de sucesos''' y se designa por {{sube|porcentaje=+20%|contenido=<math> | *Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama '''espacio de sucesos''' y se designa por {{sube|porcentaje=+20%|contenido=<math> | ||
| S\, | S\, | ||
| </math>}}.}} | </math>}}.}} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Experimento aleatorio, espacio muestral y sucesos | ||
| + | |descripcion=Actividades en las que podrás aprender los conceptos de experimento aleatorio, espacio muestral y suceso aleatorio. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena12/3quincena12_contenidos_1a.htm | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Teorema|titulo=Proposición|enunciado=Si el cardinal de {{sube|porcentaje=+20%|contenido=<math> | {{Teorema|titulo=Proposición|enunciado=Si el cardinal de {{sube|porcentaje=+20%|contenido=<math> | ||
| Línea 19: | Línea 25: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Sucesos'' | + | {{Ejemplo de sucesos}} |
| - | |enunciado= | + | |
| - | En el experimento "lanzar dos dados y anotar la suma de los puntos", determina los siguientes sucesos del espacio muestral: | + | |
| - | + | ||
| - | a) Salir múltiplo de 5.{{b4}} b) Salir número primo.{{b4}} c) Salir mayor o igual que 10. | + | |
| - | |sol= | + | |
| - | a) Salir múltiplo de 5: | + | |
| - | <math> | + | |
| - | A = | + | |
| - | \left\{ | + | |
| - | \, 5, \, 10 \, | + | |
| - | \right\} | + | |
| - | </math> | + | |
| - | | + | |
| - | + | ||
| - | <br/> | + | |
| - | + | ||
| - | b) Salir número primo: | + | |
| - | <math> | + | |
| - | B = | + | |
| - | \left\{ | + | |
| - | \, 2, \, 3, \, 5, \, 7, \, 11 \, | + | |
| - | \right\} | + | |
| - | </math> | + | |
| - | | + | |
| - | + | ||
| - | <br/> | + | |
| - | + | ||
| - | c) Salir mayor o igual que 10: | + | |
| - | <math> | + | |
| - | C = | + | |
| - | \left\{ | + | |
| - | \, 10, \, 11, \, 12 \, | + | |
| - | \right\} | + | |
| - | </math> | + | |
| - | | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ===Tipos de sucesos=== | ===Tipos de sucesos=== | ||
| - | Analicemos los tipos mas frecuentes de sucesos. | + | {{Tipos de sucesos}} |
| - | <br/> | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | *'''Sucesos elementales''' son los que están formados por un solo resultado del experimento. | + | |
| - | *'''Sucesos compuestos''' son los que estan formados por dos o más resultados del experimento, es decir, por dos o más sucesos elementales. | + | |
| - | *'''Suceso seguro''' es el que ocurre siempre que se realice el experimento aleatorio. Está formado por todos los resultados posibles del experimento y, por tanto, coincide con el espacio muestral. | + | |
| - | *'''Suceso imposible''' es el que nunca se verifica. Se representa por <math>\emptyset</math>. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ===Unión e intersección. Sucesos compatibles e incompatibles=== | + | ===Operaciones con sucesos. Sucesos compatibles e incompatibles=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *'''Unión de sucesos:''' La unión de dos sucesos <math>A\;</math> y <math>B\;</math> está formada por aquellos sucesos elementales que pertenecen al conjuto <math>A\;</math> o al conjunto <math>B\;</math> (se juntan los elementos de <math>A\;</math> y de <math>B\;</math>). Se representa <math>A \cup B</math>. | *'''Unión de sucesos:''' La unión de dos sucesos <math>A\;</math> y <math>B\;</math> está formada por aquellos sucesos elementales que pertenecen al conjuto <math>A\;</math> o al conjunto <math>B\;</math> (se juntan los elementos de <math>A\;</math> y de <math>B\;</math>). Se representa <math>A \cup B</math>. | ||
| Línea 76: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Tipos de sucesos'' | + | {{Ejemplo|titulo=Ejemplo: ''Operaciones con sucesos'' |
| |enunciado= | |enunciado= | ||
| En el experimento "lanzar un dado", se consideran los sucesos siguientes: | En el experimento "lanzar un dado", se consideran los sucesos siguientes: | ||
| Línea 88: | Línea 51: | ||
| :a) <math>A \cup B</math>{{b4}}{{b4}} b) <math>A \cap B</math>{{b4}}{{b4}} c) <math>\overline{A}</math>{{b4}}{{b4}} d) <math>\overline{B}</math> | :a) <math>A \cup B</math>{{b4}}{{b4}} b) <math>A \cap B</math>{{b4}}{{b4}} c) <math>\overline{A}</math>{{b4}}{{b4}} d) <math>\overline{B}</math> | ||
| |sol= | |sol= | ||
| + | '''Solución:''' | ||
| + | |||
| '''a)''' <math>A \cup B=\{ 1, 2, 3, 5 \}</math> | '''a)''' <math>A \cup B=\{ 1, 2, 3, 5 \}</math> | ||
| Línea 96: | Línea 61: | ||
| '''d)''' <math>\overline{B}=\{ 2, 4, 6 \}</math> | '''d)''' <math>\overline{B}=\{ 2, 4, 6 \}</math> | ||
| }} | }} | ||
| - | {´p}} | + | {{p}} |
| + | {{AI_cidead | ||
| + | |titulo1=Operaciones con sucesos | ||
| + | |descripcion=Actividades en las que podrás aprender las operaciones con sucesos. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena12/3quincena12_contenidos_1c.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Propiedades de las operaciones con sucesos | ||
| + | |descripcion=Actividades en las que podrás aprender las propiedades de las operaciones con sucesos. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena12/3quincena12_contenidos_1d.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Actividades y videotutoriales== | ==Actividades y videotutoriales== | ||
| {{Videotutoriales|titulo=Experimentos aleatorios. Espacio muestral. Sucesos|enunciado= | {{Videotutoriales|titulo=Experimentos aleatorios. Espacio muestral. Sucesos|enunciado= | ||
| Línea 135: | Línea 113: | ||
| |url1=https://www.youtube.com/watch?v=ha3iL-e-PDI&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m51s | |url1=https://www.youtube.com/watch?v=ha3iL-e-PDI&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m51s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=5'14" | ||
| + | |sinopsis='''Ejercicio 2:''' En el experimento de lanzar un dado de 6 caras, se consideran los sucesos: | ||
| + | |||
| + | :A = Sacar número par. | ||
| + | |||
| + | :B = Sacar número múltiplo de 3. | ||
| + | |||
| + | a) Halla <math>A \cup B</math>. | ||
| + | |||
| + | b) Halla <math>A \cup B</math>. | ||
| + | |||
| + | c) ¿Son A y B incompatibles? | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=LI0oWPYCzx4&index=3&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3 | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
- Llamaremos suceso de un experimento aleatorio a cada uno de los subconjuntos del espacio muestral
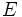 . Para designar cualquier suceso utilizaremos letras mayúsculas.
. Para designar cualquier suceso utilizaremos letras mayúsculas.
- Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama espacio de sucesos y se designa por
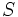 .
.
Actividades en las que podrás aprender los conceptos de experimento aleatorio, espacio muestral y suceso aleatorio.
Proposición
Si el cardinal de 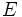 es un número finito,
es un número finito,  , entonces el cardinal de
, entonces el cardinal de 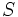 es
es 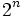
Demostración:
Como E tienen n elementos, y cada uno de ellos tiene 2 posibilidades ("estar" o "no estar" en un subconjunto de E) entonces los casos posibles son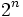 .
.Ejemplo: Sucesos
En el experimento "lanzar dos dados y anotar la suma de los puntos", determina los siguientes sucesos del espacio muestral:
a) Salir múltiplo de 5. b) Salir número primo. c) Salir mayor o igual que 10.
Solución:
a) Salir múltiplo de 5:
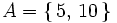
b) Salir número primo:
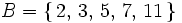
c) Salir mayor o igual que 10:
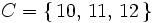
Tipos de sucesos
Analicemos los tipos mas frecuentes de sucesos.
- Sucesos elementales son los que están formados por un solo resultado o caso del experimento.
- Sucesos compuestos son los que estan formados por más de un resultado o caso del experimento, es decir, por más de un suceso elementale.
- Suceso seguro es el que ocurre siempre que se realice el experimento aleatorio. Está formado por todos los resultados posibles del experimento y, por tanto, coincide con el espacio muestral.
- Suceso imposible es el que nunca se verifica. Se representa por
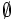 .
.
Sucesos aleatorios. Tipos.
Sucesos aleatorios. Tipos.
Operaciones con sucesos. Sucesos compatibles e incompatibles
- Unión de sucesos: La unión de dos sucesos
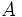 y
y 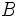 está formada por aquellos sucesos elementales que pertenecen al conjuto
está formada por aquellos sucesos elementales que pertenecen al conjuto 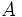 o al conjunto
o al conjunto 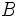 (se juntan los elementos de
(se juntan los elementos de 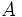 y de
y de 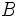 ). Se representa
). Se representa 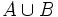 .
.
- Intersección de sucesos: La intersección de dos sucesos
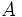 y
y 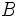 está formada por aquellos sucesos elementales que pertenecen al conjuto
está formada por aquellos sucesos elementales que pertenecen al conjuto 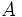 y al conjunto B (los elementos comunes de
y al conjunto B (los elementos comunes de 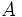 y
y 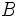 ). Se representa
). Se representa 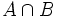 .
.
- Dos sucesos son incompatibles cuando no tienen ningún suceso elemental en común, es decir, cuando
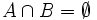 . En caso contrario diremos que son compatibles.
. En caso contrario diremos que son compatibles.
- Suceso contrario o complementario de un suceso
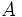 es el formado por los sucesos elementales del espacio muestral que no están en
es el formado por los sucesos elementales del espacio muestral que no están en 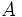 . Se representa por
. Se representa por 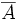 .
.
Ejemplo: Operaciones con sucesos
En el experimento "lanzar un dado", se consideran los sucesos siguientes:
- A = Obtener un número menor que 4 = {1, 2, 3}
- B = Obtener un número impar = {1, 3, 5}
Calcula:
- a)
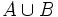 b)
b) 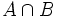 c)
c) 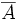 d)
d) 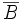
Solución:
a) 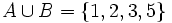
b) 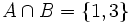
c) 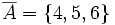
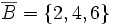
Actividades en las que podrás aprender las operaciones con sucesos.
Actividades en las que podrás aprender las propiedades de las operaciones con sucesos.
Actividades y videotutoriales
- Experimentos aleatorios. Espacio muestral. Sucesos
- Ejemplos.
La primera parte de este videotutorial de 33'20" dura 13'37" y trata sobre:
- 00:00 a 07:35: Introducción general: Experimento aleatorio, espacio muestra y sucesos.
- 07:35 a 13:35: Ejemplos de espacios muestrales y tipos de sucesos.
Ejercicio 1: En el experimento de lanzar un dado de 6 caras, calcula:
a) Espacio muestral.
b) Sucesos elementales.
c) Suceso A, "sacar un número par".
d) Suceso B, "sacar un múltiplo de 3".
e) Suceso contrario de A.
f) Suceso seguro, C y un suceso imposible, D.
Ejercicio 2: En el experimento de lanzar un dado de 6 caras, se consideran los sucesos:
- A = Sacar número par.
- B = Sacar número múltiplo de 3.
a) Halla 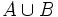 .
.
b) Halla 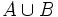 .
.
c) ¿Son A y B incompatibles?

