Plantilla:Moda
De Wikipedia
| Revisión de 09:48 4 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:55 4 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| {{Teorema_sin_demo|titulo=Cálculo de la moda con datos agrupados en intervalos|enunciado= | {{Teorema_sin_demo|titulo=Cálculo de la moda con datos agrupados en intervalos|enunciado= | ||
| - | Llamemos '''intervalo modal''' al que tiene mayor frecuencia absoluta y consideremos que todos los intervalos tienen la misma amplitud, entonces la moda viene dada por la siguiente fórmula: | + | Llamemos '''intervalo modal''' al que tiene mayor frecuencia absoluta y consideremos dos casos: |
| - | <center><math>M_o=L_i+\cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i</math></center> | + | *Todos los intervalos tienen la '''misma amplitud''', entonces la moda viene dada por la siguiente fórmula: |
| + | |||
| + | {caja|contenido=<math>M_o=L_i+\cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i</math>}} | ||
| *<math>L_i\;</math>: Extremo inferior del intervalo modal | *<math>L_i\;</math>: Extremo inferior del intervalo modal | ||
| Línea 59: | Línea 61: | ||
| *<math>A_i\;</math>: Amplitud de los intervalos. | *<math>A_i\;</math>: Amplitud de los intervalos. | ||
| + | *Todos los intervalos '''no tienen la misma amplitud''', entonces la moda viene dada por la siguiente fórmula: | ||
| + | |||
| + | {caja|contenido=<math>M_o=L_i+\cfrac{h_i-h_{i-1}}{(h_i-h_{i-1})+(h_i-h_{i+1})}\cdot A_i</math>}} | ||
| + | |||
| + | donde <math>h_i=\cfrac{f_i}{A_i}</math> son las alturas de cada intervalo. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:55 4 ago 2017
- Se define la moda como el valor de la variable que más se repite, es el decir, aquél que tiene mayor frecuencia absoluta. Se representa por Mo.
- Si hay dos o varias puntuaciones con la misma frecuencia máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
Moda Descripción: Actividades en la que podrás aprender a calcular la moda de una distribución estadística.
Actividad: Moda Descripción: Calcula en tu cuaderno la moda para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividades:
a) Modifica las frecuencias y observa como puede variar el valor de la moda.
b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable?
Moda Descripción: Ejemplos con los que podrás aprender a calcular la moda de una distribución estadística.
Autoevaluación: Moda Descripción: Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la moda de una distribución estadística.
Cálculo de la moda con datos agrupados en intervalos
Llamemos intervalo modal al que tiene mayor frecuencia absoluta y consideremos dos casos:
- Todos los intervalos tienen la misma amplitud, entonces la moda viene dada por la siguiente fórmula:
{caja
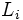: Extremo inferior del intervalo modal
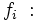Frecuencia absoluta del intervalo modal.
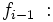Frecuencia absoluta del intervalo anterior al modal.
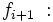Frecuencia absoluta del intervalo posterior al modal.
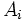: Amplitud de los intervalos.
- Todos los intervalos no tienen la misma amplitud, entonces la moda viene dada por la siguiente fórmula:
{caja|contenido=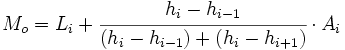
}}
donde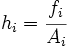 
son las alturas de cada intervalo.
}}
