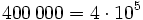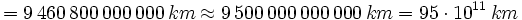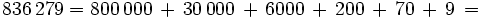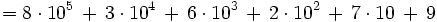Potencias de base 10 (1º ESO)
De Wikipedia
| Revisión de 16:20 10 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Descomposición polinómica de un número) |
||
| Línea 8: | Línea 8: | ||
| (Pág. 30) | (Pág. 30) | ||
| ==Expresión abreviada de números grandes== | ==Expresión abreviada de números grandes== | ||
| - | {{Teorema_sin_demo|titulo=Potencia de base 10|enunciado=:Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente | + | {{Expresión abreviada de números grandes}} |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | Esto permite expresar números grandes con muchos ceros como producto de un número por una potencia de 10. | ||
| - | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos|contenido= | ||
| - | *<math>400,000 = 4 \cdot 10^6</math> | ||
| - | *Un año luz <math> = 9,460,800,000,000 \, km \approx 9,500,000,000,000 \, km = 95 \cdot 10^11 \, km</math> | ||
| - | }} | ||
| ==Descomposición polinómica de un número== | ==Descomposición polinómica de un número== | ||
| - | {{Caja_Amarilla|texto=La '''descomposición polinómica''' de un número consiste en expresar dicho número como una suma, en la que cada sumando es cada cifra del número multiplicada por una potencia de 10, cuyo exponente es una unidad menos de la posición que ocupa la cifra que la multiplica.}} | + | {{Descomposición polinómica de un número}} |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo|contenido= | + | |
| - | *<math>836279 = 800000 \, + \, 30000 \, + \, 6000 \, + \, 200 \, + \, 70\, +\, 9\, =\, 8 \cdot 10^5 \, + \, 3 \cdot 10^4 \, + \, 6 \cdot 10^3 \, + \, 2 \cdot 10^2 \, + \, 7 \cdot 10 \, + \, 9 </math> | + | ==Ejercicios propuestos== |
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Potencias de base 10'' | ||
| + | |cuerpo= | ||
| + | (Pág. 30) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 1; 2a,b; 3; 4a,b; 5 | ||
| + | |||
| }} | }} | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 30)
Expresión abreviada de números grandes
Potencia de base 10
Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente
Esto permite expresar números grandes con muchos ceros como producto de un número por una potencia de 10.
- Un año luz
Tutorial 1 (2'38") Sinopsis:Potencias de 10.
Tutorial 2 (4'15") Sinopsis:Números naturales expresados como potencias de 10.
Autoevaluación 1 Descripción: Escribe potencias de 10 en forma de número con todas sus cifras.
Autoevaluación 2 Descripción: Expresa cantidades mediante potencias de base 10.
Autoevaluación 3 Descripción: Descomposición polinómica de un número
La descomposición polinómica de un número consiste en expresar dicho número como una suma, en la que cada sumando es cada cifra del número multiplicada por una potencia de 10, cuyo exponente es una unidad menos de la posición que ocupa la cifra que la multiplica.
Vamos a obtener la descomposición polinómica del número 836 279:
Descomposición polinómica de un número Descripción: Actividades para aprender a hallar la descomposición polinómica de un número.
Tutorial (2'46") Sinopsis: Descomposición polinómica de un número natural. Ejemplos.
Ejercicios (9'08") Sinopsis:Obtén la descomposición polinómica de los siguientes números naturales:
a) 928 b) 5400 c) 208 563 d) 86 324 642
Ejercicios propuestos
 Ejercicios propuestos: Potencias de base 10 (Pág. 30)
|
