Plantilla:Cálculo de los divisores de un número
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:06 11 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:10 8 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | + | {{Teorema_sin_demo|titulo=Propiedades de los divisores|enunciado= |
| - | *Todo número natural tiene una cantidad finita de divisores. | + | *Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo. |
| - | *Todo número natural tiene, al menos, dos divisores: 1 y él mismo. | + | *Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito. |
| - | *Para encontar todos los divisores de un número, <math>a\,</math>, buscamos las divisiones exactas {{Sube|porcentaje=15%|contenido=<math>a:b=c\,</math>}}. Entonces {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y <math>c\,</math> son divisores de <math>a\,</math>. Para ello procederemos de la siguiente manera: | + | *Si un número es divisor de otros dos, también lo es de su suma y de su diferencia. |
| + | *Si un número es divisor de otro, también lo es de cualquier múltiplo de éste. | ||
| + | *Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Cálculo de los divisores de un número=== | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| + | Para encontar todos los divisores de un número, <math>a\,</math>, buscamos las divisiones exactas {{Sube|porcentaje=15%|contenido=<math>a:b=c\,</math>}}. Entonces {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y <math>c\,</math> son divisores de <math>a\,</math>. Para ello procederemos de la siguiente manera: | ||
| #Probaremos con <math>b = 1, 2, 3, ... \,</math>. | #Probaremos con <math>b = 1, 2, 3, ... \,</math>. | ||
| #Para cada valor de {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} que dé división exacta ({{Sube|porcentaje=20%|contenido=<math>a= b \cdot k</math>}}), tendremos dos divisores: {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y {{Sube|porcentaje=15%|contenido=<math>k\,</math>}}. | #Para cada valor de {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} que dé división exacta ({{Sube|porcentaje=20%|contenido=<math>a= b \cdot k</math>}}), tendremos dos divisores: {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y {{Sube|porcentaje=15%|contenido=<math>k\,</math>}}. | ||
| #Pararemos de probar cuando el cociente de la división {{Sube|porcentaje=15%|contenido=<math>a:b\,</math>}} sea menor o igual que {{Sube|porcentaje=15%|contenido=<math>b\,</math>}}. | #Pararemos de probar cuando el cociente de la división {{Sube|porcentaje=15%|contenido=<math>a:b\,</math>}} sea menor o igual que {{Sube|porcentaje=15%|contenido=<math>b\,</math>}}. | ||
| + | |||
| }} | }} | ||
| - | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| |titulo=Ejercicio resuelto: ''Cálculo de los divisores de un número'' | |titulo=Ejercicio resuelto: ''Cálculo de los divisores de un número'' | ||
Revisión de 10:10 8 ago 2017
Propiedades de los divisores
- Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo.
- Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito.
- Si un número es divisor de otros dos, también lo es de su suma y de su diferencia.
- Si un número es divisor de otro, también lo es de cualquier múltiplo de éste.
- Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero.
Cálculo de los divisores de un número
Procedimiento
Para encontar todos los divisores de un número, 
, buscamos las divisiones exactas 
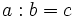. Entonces 
y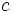 
son divisores de . Para ello procederemos de la siguiente manera:
- Probaremos con
.
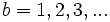- Para cada valor de que dé división exacta (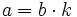
), tendremos dos divisores: y 
.
- Pararemos de probar cuando el cociente de la división
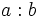sea menor o igual que .
Ejercicio resuelto: Cálculo de los divisores de un número
2. Calcula los divisores de 44.
Solución:
44 : 1 = 44 
1 y 44 son divisores. Sigo porque 44 > 1
44 :2 = 22 2 y 22 son divisores. Sigo porque 22 > 2
44 : 3 No es exacta (cociente=14). Sigo porque 14 > 3
44 : 4 = 11 4 y 11 son divisores. Sigo porque 11 > 4
44 : 5 No es exacta (cociente=8). Sigo porque 8 > 5
44 : 6 No es exacta (cociente=7). Sigo porque 7 > 6
44 : 7 No es exacta (cociente=6). Paro porque 6 < 7
