Plantilla:Máximo común divisor
De Wikipedia
| Revisión de 11:05 8 ago 2017 Coordinador (Discusión | contribuciones) (→Cálculo del máximo común divisor) ← Ir a diferencia anterior |
Revisión de 11:06 8 ago 2017 Coordinador (Discusión | contribuciones) (→Propiedades) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| El '''máximo común divisor''' (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.}} | El '''máximo común divisor''' (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.}} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | ||
| {{Teorema_sin_demo|titulo=Propiedad|enunciado=Si ''a'' es múltiplo de ''b'', entonces ''m.c.d.''(''a,b'')=''b''.}} | {{Teorema_sin_demo|titulo=Propiedad|enunciado=Si ''a'' es múltiplo de ''b'', entonces ''m.c.d.''(''a,b'')=''b''.}} | ||
| {{p}} | {{p}} | ||
| Línea 8: | Línea 7: | ||
| :m.c.d.(15, 30)=15, porque 30 es múltiplo de 15.}} | :m.c.d.(15, 30)=15, porque 30 es múltiplo de 15.}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Cálculo del máximo común divisor== | ==Cálculo del máximo común divisor== | ||
| {{Teorema_sin_demo|titulo=Procedimiento | {{Teorema_sin_demo|titulo=Procedimiento | ||
Revisión de 11:06 8 ago 2017
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Propiedad
Si a es múltiplo de b, entonces m.c.d.(a,b)=b.
- m.c.d.(15, 30)=15, porque 30 es múltiplo de 15.
Tabla de contenidos |
Cálculo del máximo común divisor
Procedimiento
Para obtener el m.c.d. de varios números, se descomponen los números en factores primos y se toman los factores comunes elevados al menor exponente.
- Calcula el m.c.d.(24,60).
- Primer método:
- Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
- Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- m.c.d.(24,60)= 12
- Segundo método:
- Descomponemos 24 y 60 en sus factores primos:
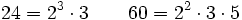
- Multiplicando los factores comunes elevados al menor exponente:
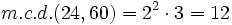
Tutorial (13´46") Sinopsis:Tutorial que explica el significado del máximo común divisor, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los divisores de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 07:33: ¿Qué es el Mínimo Común Múltiplo? Método de extracción de divisores.
- 07:33 a 13:46: Método general para calcular el MCD. Ejemplos.
Ejercicio 1 (6'19") Sinopsis:Cálcula el máximo común divisor de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Ejercicio 2 (5'52") Sinopsis: Cálcula el máximo común divisor de:
a) 30 y 45
b) 36, 84 y 120
Ejercicio 3 (14'59") Sinopsis: Cálcula el máximo común divisor de:
a) 18 y 24
b) 36, 54 y 90
Algoritmo de Euclides
Algoritmo de Euclides
El algoritmo de Euclides es un procedimiento para calcular el m.c.d. de dos números. Los pasos son:
Se divide el número mayor entre el menor.
- Si la división es exacta, el divisor es el m.c.d.
- Si la división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m.c.d.
Números primos entre sí
Dos números son primos entre sí, si su m.c.d. es 1.
- 6 y 11 son primos entre sí.
Propiedades
Si a y b son primos entre sí, entonces m.c.m.(a,b)=a · b.
- Como 6 y 11 son primos entre sí, entonces m.c.m(6,11)=6·11=66
Actividades
Máximo común divisor de dos números Descripción: Actividad en la que podrás obtener el m.c.d. de dos números por el método artesanal.
- Actividad en la que podrás obtener el m.c.d. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.d. de dos números por descomposición factorial.
Actividad: Máximo común divisor
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio resuelto: m.c.d.
En un almacén quieren envasar, para su distribución, 200 kg de manzanas y 260 kg de de naranjas, en cajones del mismo peso y de la mayor carga que sea posible. ¿Cuántos kilos deben poner en cada cajón?
- Solucuión: 20 kg
