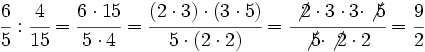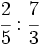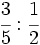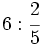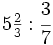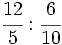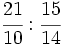Multiplicación y división de fracciones (2º ESO)
De Wikipedia
| Revisión de 17:12 30 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:24 30 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 72) | (Pág. 72) | ||
| {{p}} | {{p}} | ||
| - | + | ==Multiplicación y división de fracciones== | |
| + | {{Introducción a la multiplicación y división de fracciones}} | ||
| + | {{p}} | ||
| + | ===Multiplicación de fracciones=== | ||
| + | {{Multiplicacion fracciones}} | ||
| + | {{p}} | ||
| + | {{Ejemplo multiplicación fracciones}} | ||
| + | {{p}} | ||
| + | {{actividades multiplicacion fracciones}} | ||
| + | {{p}} | ||
| + | {{wolfram multiplicacion fracciones}} | ||
| + | {{p}} | ||
| + | ===Inversa de una fracción=== | ||
| + | {{Inversa de una fracción}} | ||
| + | {{p}} | ||
| + | ===División de fracciones=== | ||
| + | {{Division fracciones}} | ||
| + | {{p}} | ||
| + | No obstante, es conveniente simplificar antes de efectuar los productos.{{p}} | ||
| + | {{p}} | ||
| + | {{Ejemplo division fracciones}} | ||
| + | {{p}} | ||
| + | {{actividades division fracciones}} | ||
| + | {{p}} | ||
| + | {{wolfram division fracciones}} | ||
| + | {{p}} | ||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 17:24 30 ago 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 72)
Multiplicación y división de fracciones
Videotutorial sobre la multiplicación y división de fracciones.
Tutorial que explica la multiplicación y división con fracciones de manera simple y en forma combinada, trabajando la simplificación previa.
Actividades en las que aprenderás la multiplicación de fracciones y sus propiedades.
Multiplicación de fracciones
Procedimiento: Multiplicación de fracciones
Para multiplicar fracciones, se pone como numerador, el producto de los numeradores, y como denominador, el producto de los denominadores.
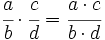
- Si en una multiplicación de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para multiplicar números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, la forma en que se realiza el producto de dos fracciones permite, en ocasiones, simplificar antes de realizar las multiplicaciones de los numeradores y denominadores. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo: Multiplicación de fracciones
Calcula: 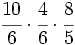
Solución:
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto: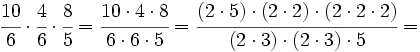
Aprende a multiplicar fracciones.
Aprende a multiplicar fracciones.
Aprende a multiplicar números naturales por fracciones.
Significado gráfico de la multiplicación de dos fracciones.
Representación en la recta numérica de la multiplicación de dos fracciones.
Aprende a multiplicar números por fracciones.
- Multiplicación de fracciones.
- Ejemplos.
- Propiedades.
Multiplica:
Multiplica:
a) 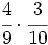 b)
b) 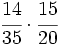 c)
c) 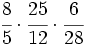
Multiplica un entero por una fracción:
a) 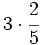
b) 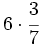
Multiplica fracciones mixtas con fracciones y enteros:
Multiplica:
Compara las siguientes fracciones sin hacer la multiplicación:
Multiplica:
Para elaborar cierto pastel, la receta dice que por cada libra se debe usar 1 taza y 3/4 de almendras. Si nos encargan un pastel de 3 libras y media, ¿cuántas tazas de almendras son necesarias?
Una receta para pastelillos de plátano y avena requiere 3/4 tazas de avena. Si preparamos 1/2 de la receta, ¿cuánta avena necesitaremos?
Gina tenía 2/3 de taza de detergente. Si usó la mitad el viernes para lavar todas sus sábanas, ¿Cuánto le sobra?.
Puedes andar en bicicleta 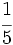 de milla por minuto. Si tardas
de milla por minuto. Si tardas 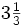 de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
Actividades en las que aprenderás y practicarás la multiplicación de fracciones.
Actividades para practicar la multiplicación de fracciones.
Inversa de una fracción
- Dos fracciones son inversas cuando su producro es la unidad.
- Toda fracción
 , distinta de cero, tiene inversa. Su inversa es la fracción
, distinta de cero, tiene inversa. Su inversa es la fracción 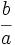 .
.
La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa.
Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados.
Pulsa "inicio" para que aparezca otra fracción.
División de fracciones
Procedimiento: División de fracciones
Para dividir dos fracciones, se multiplica la primera fracción por la inversa de la segunda.
El resultado es otra fracción, cuyo numerador, es el producto del primer numerador por el segundo denominador, y cuyo denominador es el producto del primer denominador por el segundo numerador.
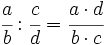
- Si en una división de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para dividir números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, al igual que ocurre con la multiplicación de fracciones, en ocasiones, podremos simplificar antes de efectuar los productos cruzados de los numeradores y denominadores. Lo que haremos es dejar indicados los productos cruzados y simplificarlos, si es posible, antes de multiplicarlos. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo:
Calcula: 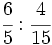
Solución:
Multiplicamos en cruz, simplificando antes de efectuar el producto:Aprende a dividir fracciones.
Aprende a dividir fracciones.
Aprende a dividir fracciones (2 métodos). Ejercicios propuestos y resueltos.
División de dos fracciones usando la fracción inversa. Ejemplos.
- División de fracciones.
- Ejemplos.
- Ejercicios con operaciones combinadas.
División de fracciones. Ejemplo.
Cómo se dividen las fracciones. Ejemplos.
Equivalencias fundamentales en la multiplicación y división de fracciones.
Fracciones de términos no enteros y fracciones de términos racionales
Simplificación de fracciones de términos racionales.
Las propiedades de la división de fracciones
Entendiendo el concepto de división de fracciones
Calcula:
Calcula y expresa la solución como un número mixto:
Calcula:
- 1)
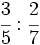 ; 2)
; 2) 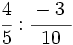 ; 3)
; 3) 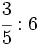 ; 4)
; 4) 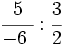
- 5)
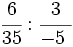 ; 6)
; 6) 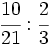 ; 7)
; 7) 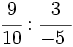
Calcula:
- 8)
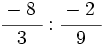 ; 9)
; 9) 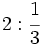 ; 10)
; 10) 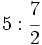
- 11)
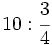 ; 12)
; 12) 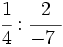 ; 13)
; 13) 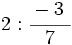
Corrige esta cuenta si crees que es incorrecta:
- 14)
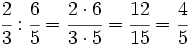
Calcula:
- 15)
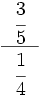 ; 16)
; 16)  ; 17)
; 17) 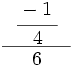 ; 18)
; 18) 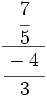
- 19)
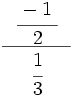 ; 20)
; 20) 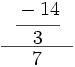 ; 21)
; 21) 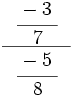
Calcula:
- 22)
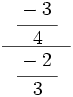 ; 23)
; 23) 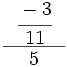 ; 24)
; 24) 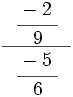
- 25)
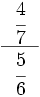 ; 26)
; 26) 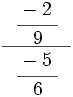 ; 27)
; 27) 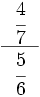
Escribe la fracción que falta para que se verifique la igualdad:
- 52)
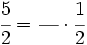
- 53)
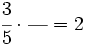
División de fracciones.
a) 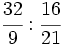 b)
b) 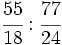
Divide un entero por una fracción:
Divide fracciones mixtas con fracciones:
En la fiesta de cumpleaños de Luisa ha sobrado 1/3 del pastel. Jaime lo ha visto y, como tenía hambre, se ha comido la mitad. ¿Qué parte o fracción de pastel se ha comido Jaime?. ¿Qué parte o fracción del pastel sobra?
La camiseta de un bebe se fabrica con 4/5 metros de tela. ¿Cuántas camisetas se pueden hacer con 48 metros de tela?
Actividades en las que aprenderás y practicarás la división de fracciones.
Actividades para practicar la división de fracciones.
Actividades para practicar la división de fracciones.
Ejercicios propuestos
|
Ejercicios propuestos: Multiplicación y división de fracciones |
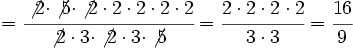
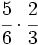
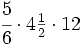
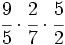
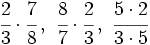
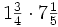
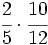
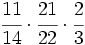
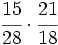
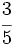 es
es 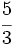 .
.
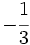 es
es 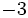 .
.