Plantilla:Razón y proporción 1ºESO
De Wikipedia
| Revisión de 16:55 4 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:57 4 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 46: | Línea 46: | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| - | Para calcular el cuarto proporcional aplicaremos la propiedad de las fracciones equivalentes que dice que ''el producto de extremos es igual al producto de medios'', y despejaremos la incógnita: | + | Para calcular el cuarto proporcional aplicaremos la propiedad de las fracciones equivalentes que dice que ''"el producto de extremos es igual al producto de medios"'', y despejaremos la incógnita: |
| <center><math>\cfrac{a}{b}=\cfrac{c}{x} \quad\Leftrightarrow\quad a \cdot x=b \cdot c \quad\Leftrightarrow\quad x=\cfrac{b \cdot c}{a}</math></center> | <center><math>\cfrac{a}{b}=\cfrac{c}{x} \quad\Leftrightarrow\quad a \cdot x=b \cdot c \quad\Leftrightarrow\quad x=\cfrac{b \cdot c}{a}</math></center> | ||
Revisión de 16:57 4 sep 2017
Proporciones numéricas (14'16") Sinopsis:Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción. -
- 00:00 a 02:40: Introducción (ejemplos).
- 02:40 a 03:15: Definición de razón de proporción entre dos cantidades (números).
- 03:15 a 05:24: Ejemplos 1-2-3 de razón de proporción entre dos números.
- 05:24 a 08:15: Ejemplo 4 de aplicación de razón.
- 08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos. - 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón.
Estamos acostumbrados a dar información sobre situaciones de la vida cotidiana usando números. Hay ocasiones en las que un solo número no es suficiente y debemos compararlo con otra cantidad para poder comprender mejor la situación. Cuando comparamos dos cantidades formamos una razón.
Razón es el cociente entre dos números 
y 
. Se escribe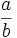 
y se lee " es a ".
Una razón no tiene unidades y sirve para comparar, ya que indica el nº de veces que una cantidad es mayor que otra.
Razón entre dos números Descripción: - En una primera escena te presentamos varios ejemplos de razón entre dos números para entender qué nos indica.
- En otra actividad te proponemos que halles la razón en tres casos concretos.
Una proporción es una igualdad entre dos razones: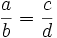 
.
Proporción Descripción: - En una primera escena te presentamos varios ejemplos de proporciones.
- En otra actividad te proponemos que compruebes si dos razones dadas forman o no una proporción.
Autoevaluación: Proporciones Descripción: Ejercicios de autoevaluación sobre proporciones.
Se llama cuarto proporcional al término que desconocemos en una proporción.
Dado que el producto de medios es igual al de extremos, podemos calcular cualquier término de una proporción conociendo los otros tres.
Procedimiento
Para calcular el cuarto proporcional aplicaremos la propiedad de las fracciones equivalentes que dice que "el producto de extremos es igual al producto de medios", y despejaremos la incógnita:
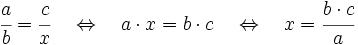
Cálculo del cuarto proporcional Descripción: Actividades para aprender y practicar el cálculo del cuarto proporcional.
Autoevaluación: Cuarto proporcional Descripción: Ejercicios de autoevaluación sobre cuartos proporcionales.
